题目内容
17.已知椭圆焦点在x轴上,下顶点为D(0,-1),且离心率$e=\frac{{\sqrt{6}}}{3}$.经过点M(1,0)的直线L与椭圆交于A,B两点.(Ⅰ)求椭圆的标准方程;
(Ⅱ)求|AM|的取值范围.
(Ⅲ)在x轴上是否存在定点P,使∠MPA=∠MPB.若存在,求出点P的坐标,若不存在,说明理由.
分析 (Ⅰ)设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$由已知得$b=1,\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,又a2=b2+c2,∴a2=3,b2=1,
(Ⅱ) 设A(x1,y1),用x1,y1表示|AM|,再利用$\frac{x_1^2}{3}+y_1^2=1$,求出|AM|的最小值.
(Ⅲ)假设x轴上存在定点P(m,0)满足条件,B(x2,y2).当直线L的斜率存在时,设直线L方程为:y=k(x-1)由$\left\{\begin{array}{l}\frac{x^2}{3}+{y^2}=1\\ y=k(x-1)\end{array}\right.$消去y整理得,(1+3k2)x2-6k2x+3k2-3=0${x_1}+{x_2}=\frac{{6{k^2}}}{{1+3{k^2}}},{x_1}•{x_2}=\frac{{3{k^2}-3}}{{1+3{k^2}}}$,由∠MPA=∠MPB得kPA+kPB=0,即可.
解答 解:(Ⅰ)设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$由已知得$b=1,\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,
又a2=b2+c2,∴a2=3,b2=1,即椭圆方程为$\frac{x^2}{3}+{y^2}=1$…(2分)
(Ⅱ) 设A(x1,y1),
即$\frac{x_1^2}{3}+y_1^2=1$,$|AM|=\sqrt{{{({x_1}-1)}^2}+y_1^2}=\sqrt{x_1^2-2{x_1}+1+(1-\frac{x^2}{3})}=\sqrt{\frac{{2{x^2}}}{3}-2{x_1}+2}$
又$-\sqrt{3}≤x≤\sqrt{3}$,得$\frac{{2{x^2}}}{3}-2{x_1}+2=\frac{2}{3}{(x-\frac{3}{2})^2}+\frac{1}{2}≥\frac{1}{2}$
∴所以当x1=时,|AM|的最小值为$\frac{1}{2}$…6分
(Ⅲ)假设x轴上存在定点P(m,0)满足条件,B(x2,y2).
当直线L的斜率存在时,设直线L方程为:y=k(x-1)
由$\left\{\begin{array}{l}\frac{x^2}{3}+{y^2}=1\\ y=k(x-1)\end{array}\right.$消去y整理得,(1+3k2)x2-6k2x+3k2-3=0${x_1}+{x_2}=\frac{{6{k^2}}}{{1+3{k^2}}},{x_1}•{x_2}=\frac{{3{k^2}-3}}{{1+3{k^2}}}$…(8分)
由∠MPA=∠MPB得kPA+kPB=0,即$\frac{{{x_1}-1}}{y_1}+\frac{{{x_2}-1}}{y_2}=0$,…(8分)
又y1=k(x1-1),y2=k(x2-1)即$\frac{{{x_1}-m}}{y_1}+\frac{{{x_2}-m}}{y_2}=\frac{{{x_1}-m}}{{k({x_1}-1)}}+\frac{{{x_2}-m}}{{k({x_2}-1)}}=\frac{{2{x_1}{x_2}-(m+1)({x_1}+{x_2})+2m}}{{{k^2}({x_1}-1)({x_2}-1)}}$=0.
$2×\frac{{3{k^2}-3}}{{1+3{k^2}}}-(m+1)\frac{{6{k^2}}}{{1+3{k^2}}}+2m=\frac{-6+2m}{{1+3{k^2}}}=0$,
即m=3,P(3,0)
当直线L的斜率不存在时,也满足条件.
∴定点P坐标为(3,0)…(12分)
点评 本题考查了椭圆的方程,直线与椭圆的位置关系、范围问题、定点问题,转化思想是解题关键,属于中档题.

 阅读快车系列答案
阅读快车系列答案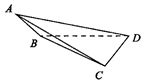 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
| A. | ±2 | B. | -2 | C. | ±4 | D. | 4 |
| A. | 5 | B. | 6 | C. | 4 | D. | 8 |
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{c}$ |
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点. 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.