题目内容
7.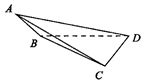 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
分析 由题意,面积为S4的三角形在平面α上的射影为△OAC,即可得出结论.
解答  解:如图所示,面积为S4的三角形在平面α上的射影为△OAC,
解:如图所示,面积为S4的三角形在平面α上的射影为△OAC,
面积为$\frac{1}{2}×\sqrt{25+9}×4$=2$\sqrt{34}$,
故选A.
点评 本题考查射影的概念,考查三角形面积的计算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知点A($\sqrt{3}$,2),B(0,3),C(0,1),则∠BAC=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
12.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{3}{2}$ |
19.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右顶点分别为A1,A2,左右焦点分别为F1,F2,以F1F2为直径的圆与双曲线左支的一个交点为P,若以A1A2为直径的圆与PF2相切,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
16.当双曲线M:$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{2m+4}$=1(-2<m<0)的焦距取得最小值时,双曲线M的渐近线方程为( )
| A. | y=±$\sqrt{2}x$ | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
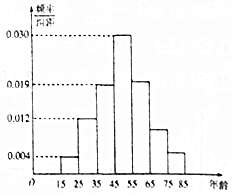 2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:
2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示: