题目内容
5.已知点M(4,t)在抛物线x2=4y上,则点M到焦点的距离为( )| A. | 5 | B. | 6 | C. | 4 | D. | 8 |
分析 把点M(4,t)代入抛物线方程,解得t.利用抛物线的定义可得:点M到抛物线焦点的距离=t+1.
解答 解:把点M(4,t)代入抛物线方程可得:16=4t,解得t=4.
∴点M到抛物线焦点的距离=4+1=5.
故选A.
点评 本题考查了抛物线的定义标准方程及其性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
16.当双曲线M:$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{2m+4}$=1(-2<m<0)的焦距取得最小值时,双曲线M的渐近线方程为( )
| A. | y=±$\sqrt{2}x$ | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
14.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),则下列向量中与向量2$\overrightarrow{a}$+$\overrightarrow{b}$垂直的是( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
15.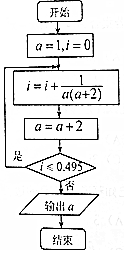 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )
 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
 某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.
某次数学测验,12名同学分数的茎叶图如图:则这些分数的中位数是80.