题目内容
12. 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.(Ⅰ)求证:直线MN∥平面ABCD.
(Ⅱ)求B1到平面A1BC1的距离.
分析 (Ⅰ)连结B1C、AC,则N也是B1C的中点,证明MN∥AC,利用线面平行的判定定理证明MN∥平面ABCD;
(Ⅱ)由${v_{{B_1}-{A_1}B{C_1}}}={v_{{A_1}-{B_1}BC}}_1$,求出B1到平面A1BC1的距离.
解答 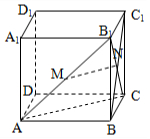 (Ⅰ)证明:连结B1C、AC,则N也是B1C的中点
(Ⅰ)证明:连结B1C、AC,则N也是B1C的中点
∴MN是△B1AC的中位线,即有MN∥AC…3
∵MN?平面ABCD,AC?平面ABCD
∴MN∥平面ABCD…(5分)
(Ⅱ)解:△A1BC1是边长为$\sqrt{2}$的等边三角形,∴${S_{△{A_1}BC{\;}_1}}=\frac{1}{2}×\sqrt{2}×\sqrt{2}×sin{60^0}=\frac{{\sqrt{3}}}{2}$…(7分)
设B1到平面A1BC1的距离为h,由${v_{{B_1}-{A_1}B{C_1}}}={v_{{A_1}-{B_1}BC}}_1$
得$\frac{1}{3}×\frac{{4\sqrt{3}h}}{4}=\frac{1}{3}×(1×1×\frac{1}{2})×1$,∴$h=\frac{{\sqrt{3}}}{3}$…(10分)
点评 本题考查线面平行的判定定理,考查B1到平面A1BC1的距离,考查学生的计算能力,考查学生分析解决问题的能力,正确运用线面平行的判定定理是关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.执行如图所示程序框图,若使输出的结果不大于100,则输入的整数k的最大值为( )

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.设△ABC的内角A,B,C分别对应边a,b,c.若c2=(a-b)2+6,${S_{△ABC}}=\frac{3}{2}\sqrt{3}$,则角C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{3}{4}π$ | D. | $\frac{2}{3}π$ |
1.已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),若对任意实数x都有x2f′(x)>2xf(-x),则不等式x2f(x)<(3x-1)2f(1-3x)的解集是( )
| A. | ($\frac{1}{4}$,+∞) | B. | (0,$\frac{1}{4}$) | C. | (-∞,$\frac{1}{4}$) | D. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) |
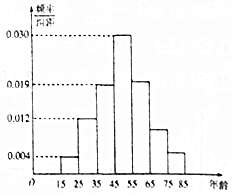 2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:
2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示: