题目内容
11.在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F,且与该抛物线相交于A,B两点,其中点A在x轴上方.若直线l的倾斜角为60°,则|OA|=$\sqrt{21}$.分析 由题意可知求得直线l的方程,代入抛物线方程,点A在x轴上方,即可求得A点坐标,利用两点之间的距离公式,即可求得丨OA丨.
解答 解:抛物线y2=4x的焦点F的坐标为(1,0)
∵直线l过F,倾斜角为60°,即斜率k=tanα=$\sqrt{3}$,
∴直线l的方程为:y=$\sqrt{3}$(x-1),即x=$\frac{\sqrt{3}}{3}$y+1,
$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}y+1}\\{{y}^{2}=4x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{y=2\sqrt{3}}\\{x=3}\end{array}\right.$,$\left\{\begin{array}{l}{y=-\frac{2\sqrt{3}}{3}}\\{x=\frac{1}{3}}\end{array}\right.$,
由点A在x轴上方,则A(3,2$\sqrt{3}$),
则|OA|=$\sqrt{(3)^{2}+(2\sqrt{3})^{2}}$=$\sqrt{21}$,
则丨OA丨=$\sqrt{21}$,
故答案为:$\sqrt{21}$.
点评 本题考查直线与抛物线的位置关系,考查直线的点斜式方程,考查计算能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.已知集合A={y|0≤y<2,y∈N},B={x|x2-4x-5≤0,x∈N},则A∩B=( )
| A. | {1} | B. | {0,1} | C. | [0,2) | D. | ∅ |
16.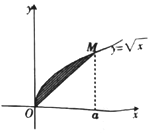 如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
 如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
3.企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的8%缴纳,某企业员工甲在2010年至2016年各年中每月所缴纳的养老保险数额y(单位:元)与年份序号t的统计如表:
(1)求y关于t的线性回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
20.若${(x-\frac{1}{x})}^{n}$的展开式中只有第7项的二项式系数最大,则展开式中含x2项的系数是( )
| A. | -462 | B. | 462 | C. | 792 | D. | -792 |
 从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.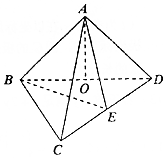 如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.
如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.