题目内容
1．已知集合A={y|0≤y＜2，y∈N}，B={x|x2-4x-5≤0，x∈N}，则A∩B=（ ）| A． | {1} | B． | {0，1} | C． | [0，2） | D． | ∅ |
分析 化简集合A、B，根据交集的定义写出A∩B．
解答 解：集合A={y|0≤y＜2，y∈N}={0，1}，
B={x|x2-4x-5≤0，x∈N}={x|-1≤x≤5，x∈N}={0，1，2，3，4，5}，
则A∩B={0，1}．
故选：B．
点评 本题考查了集合的化简与运算问题，是基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
11．平行四边形ABCD中，AB=2，AD=1，$\overrightarrow{AB}$•$\overrightarrow{AD}$=-1，点M在边CD上，则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最大值为（ ）
| A． | 2 | B． | 2$\sqrt{2}$-1 | C． | 5 | D． | $\sqrt{3}$-1 |
16．已知集合A={-1，0，1，2，3}，B={x|x＜2}，则A∩B=（ ）
| A． | {-1，0，1} | B． | {0，1，2} | C． | {0，1，2，3} | D． | {-1，0，1，2，3} |
6．设集合A={x|x（5-x）＞4}，B={x|x≤a}，若A∪B=B，则a的值可以是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
13．
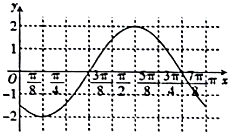函数f（x）=Asin（ωx+φ）（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向右平移$\frac{7π}{24}$个单位后得到函数g（x）的图象，若函数g（x）在区间$[{-\frac{π}{3}，θ}]$（$θ＞-\frac{π}{3}$）上的值域为[-1，2]，则θ等于（ ）
函数f（x）=Asin（ωx+φ）（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向右平移$\frac{7π}{24}$个单位后得到函数g（x）的图象，若函数g（x）在区间$[{-\frac{π}{3}，θ}]$（$θ＞-\frac{π}{3}$）上的值域为[-1，2]，则θ等于（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{7π}{12}$ |
10．（x2-$\frac{2}{x}$+y）5的展开式中，含x3y2的项的系数为（ ）
| A． | 60 | B． | -60 | C． | 80 | D． | -80 |