题目内容
16.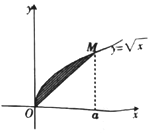 如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
分析 利用定积分的几何意义表示曲边梯形的面积,然后计算.
解答 解:由题意,M(a,$\sqrt{a}$),直线OM的方程为y=$\frac{x}{\sqrt{a}}$
故所求图形的面积为S=∫0a($\sqrt{x}$-$\frac{x}{\sqrt{a}}$)dx
=($\frac{2}{3}{x}^{\frac{3}{2}}$-$\frac{{x}^{2}}{2\sqrt{a}}$)|0a=$\frac{1}{6}{a}^{\frac{3}{2}}$=$\frac{1}{6}$,
∴a=1,
故选:C.
点评 本题考查了利用定积分求封闭图形的面积;关键是正确利用定积分表示面积.

练习册系列答案
相关题目
6.设集合A={x|x(5-x)>4},B={x|x≤a},若A∪B=B,则a的值可以是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.已知集合A={x|x2-9≤0},B={x|y=ln(-x2+x+12)},则A∩B=( )
| A. | {x|-3≤x<3} | B. | {x|-2<x≤0} | C. | {x|-2<x<0} | D. | {x|x<0或x>2且x≠3} |
8.f(x)=$\sqrt{x}$lnx在点(4,f(4))处的切线方程为( )
| A. | (ln2+1)x-2y+4ln2-4=0 | B. | (ln4+1)x-2y+7ln4-1=0 | ||
| C. | (ln4+1)x-2y+8ln2-4=0 | D. | (ln2+1)x+2y+7ln2-4=0 |
6.已知F1、F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$],∠F1PF2=$\frac{π}{2}$,则双曲线C2的离心率e2的最小值为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |