题目内容
3．企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的8%缴纳，某企业员工甲在2010年至2016年各年中每月所缴纳的养老保险数额y（单位：元）与年份序号t的统计如表：| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
（2）按照这种变化趋势，利用（1）中回归方程，预测2017年该员工每月的平均工资（精确到0.1）．
参考公式和数据：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$，$\sum_{i=1}^{7}$tiyi=13860，$\sum_{i=1}^{7}$ti2=140．
分析 （1）根据数据求出样本平均数以及对应的系数即可求y关于t的线性回归方程；
（2）根据条件进行估计预测即可得到结论．
解答 解：（1）∵$\overline{t}$=4，$\overline{y}$=440，$\sum_{i=1}^{7}$tiyi=13860，$\sum_{i=1}^{7}$ti2=140…（3分），
∴$\widehat{b}$=$\frac{13860-7×4×440}{140-7×16}$=55，$\widehat{a}$=220，所求回归方程为$\widehat{y}$=55t+220（3分）．
（2）将t=8代入（1）中的回归方程，得$\widehat{y}$=55×8+220=660，
故预测2017年该员工每月的平均工资为$\frac{660}{0.08}$=8250．…（2分）．
点评 本题主要考查线性回归方程的求解以及应用，根据数据求出相应的系数是解决本题的关键．考查学生的运算能力．
练习册系列答案
阅读快车系列答案
相关题目
13．
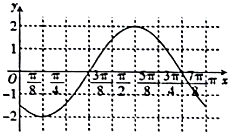函数f（x）=Asin（ωx+φ）（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向右平移$\frac{7π}{24}$个单位后得到函数g（x）的图象，若函数g（x）在区间$[{-\frac{π}{3}，θ}]$（$θ＞-\frac{π}{3}$）上的值域为[-1，2]，则θ等于（ ）
函数f（x）=Asin（ωx+φ）（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向右平移$\frac{7π}{24}$个单位后得到函数g（x）的图象，若函数g（x）在区间$[{-\frac{π}{3}，θ}]$（$θ＞-\frac{π}{3}$）上的值域为[-1，2]，则θ等于（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{7π}{12}$ |
18．现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标，若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为$\frac{5}{6}$，那么9个空气净化器中甲、乙品牌个数分布可能是（ ）
| A． | 甲品牌1个，乙品牌8个 | B． | 甲品牌2个，乙品牌7个 | ||
| C． | 甲品牌3个，乙品牌6个 | D． | 甲品牌4个，乙品牌5个 |
8．f（x）=$\sqrt{x}$lnx在点（4，f（4））处的切线方程为（ ）
| A． | （ln2+1）x-2y+4ln2-4=0 | B． | （ln4+1）x-2y+7ln4-1=0 | ||
| C． | （ln4+1）x-2y+8ln2-4=0 | D． | （ln2+1）x+2y+7ln2-4=0 |
12．已知全集U={0，1，2，3，4}，A={1，3}，B={0，1，4}，则（∁UA）∩B=（ ）
| A． | {0，1，2，4} | B． | {2，3} | C． | {2，4} | D． | {0，4} |
