题目内容
20．若${（x-\frac{1}{x}）}^{n}$的展开式中只有第7项的二项式系数最大，则展开式中含x2项的系数是（ ）| A． | -462 | B． | 462 | C． | 792 | D． | -792 |
分析 先由条件求得n=12，在二项展开式的通项公式中，令x的幂指数等于2，求出r的值，即可求得x2的系数．
解答 解：${（x-\frac{1}{x}）}^{n}$的展开式中只有第7项的二项式系数最大，∴n=12，
通项为Tr+1=$（-1）^{r}{C}_{12}^{r}{x}^{12-2r}$，令12-2r=2，∴r=5，
∴展开式中含x2项的系数是$（-1）^{5}{C}_{12}^{5}$=-792，
故选：D．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
10．（x2-$\frac{2}{x}$+y）5的展开式中，含x3y2的项的系数为（ ）
| A． | 60 | B． | -60 | C． | 80 | D． | -80 |
8．f（x）=$\sqrt{x}$lnx在点（4，f（4））处的切线方程为（ ）
| A． | （ln2+1）x-2y+4ln2-4=0 | B． | （ln4+1）x-2y+7ln4-1=0 | ||
| C． | （ln4+1）x-2y+8ln2-4=0 | D． | （ln2+1）x+2y+7ln2-4=0 |
12．已知全集U={0，1，2，3，4}，A={1，3}，B={0，1，4}，则（∁UA）∩B=（ ）
| A． | {0，1，2，4} | B． | {2，3} | C． | {2，4} | D． | {0，4} |
9．
阅读右边的程序框图，运行相应的程序，输出k的值是（ ）
阅读右边的程序框图，运行相应的程序，输出k的值是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
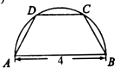如图，将一块半径为2的半圆形纸板切割成等腰梯形的形状，下底AB是半圆的直径，上底CD的端点在半圆上，则所得梯形的最大面积为3$\sqrt{3}$．