题目内容
2.关于x的方程$({k-7}){x^2}+4lnx-\frac{1}{x^2}+k=0$有两个不等实根,则实数k的取值范围是(4,7).分析 分离参数k=$\frac{7{x}^{2}+\frac{1}{{x}^{2}}-4lnx}{{x}^{2}+1}$,求出右侧函数的单调性和最值或极限,从而得出k的范围.
解答 解:∵$({k-7}){x^2}+4lnx-\frac{1}{x^2}+k=0$有两解,
∴k=$\frac{7{x}^{2}+\frac{1}{{x}^{2}}-4lnx}{{x}^{2}+1}$有两解,
令f(x)=$\frac{7{x}^{2}+\frac{1}{{x}^{2}}-4lnx}{{x}^{2}+1}$,则f′(x)=$\frac{8xlnx+10x-\frac{8}{x}-\frac{2}{{x}^{3}}}{({x}^{2}+1)^{2}}$,
∴当0<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=1时,f(x)取得最小值f(1)=4,
又x→0时,f(x)→+∞,x→+∞时,f(x)→7,
∴4<k<7.
故答案为(4,7).
点评 本题考查了方程根的个数与函数单调性的关系,函数最值的计算,属于中档题.

练习册系列答案
相关题目
13.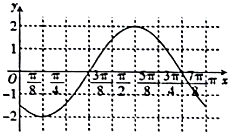 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{7π}{12}$ |
10.(x2-$\frac{2}{x}$+y)5的展开式中,含x3y2的项的系数为( )
| A. | 60 | B. | -60 | C. | 80 | D. | -80 |
7.已知集合A={x|x2-9≤0},B={x|y=ln(-x2+x+12)},则A∩B=( )
| A. | {x|-3≤x<3} | B. | {x|-2<x≤0} | C. | {x|-2<x<0} | D. | {x|x<0或x>2且x≠3} |
12.已知全集U={0,1,2,3,4},A={1,3},B={0,1,4},则(∁UA)∩B=( )
| A. | {0,1,2,4} | B. | {2,3} | C. | {2,4} | D. | {0,4} |