题目内容
17．若复数z1，z2在复平面内的对应点关于实轴对称，z1=2-i，则z1•z2=（ ）| A． | -5 | B． | 5 | C． | -4+i | D． | -4-i |
分析 复数z1，z2在复平面内的对应点关于实轴对称，z1=2-i，可得z2=2+i．再利用复数的运算法则即可得出．
解答 解：∵复数z1，z2在复平面内的对应点关于实轴对称，z1=2-i，∴z2=2+i．
则z1•z2=（2-i）（2+i）=22+12=5．
故选：B．
点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
12．
已知an=（$\frac{1}{3}$）n，把数列{an}的各项排成如图的三角形，记A（s，t）表示第s行的第t个数，则A（11，12）=（ ）
已知an=（$\frac{1}{3}$）n，把数列{an}的各项排成如图的三角形，记A（s，t）表示第s行的第t个数，则A（11，12）=（ ）| A． | （$\frac{1}{3}$）67 | B． | （$\frac{1}{3}$）68 | C． | （$\frac{1}{3}$）112 | D． | （$\frac{1}{3}$）113 |
2．
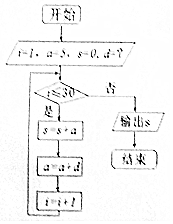《九章算术》之后，人们学会了用数列的知识来解决问题．公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为：“今有女善织，日益功疾，初日织五尺，今一月织九匹三丈．问日益几何？”．利用这种思想设计的一个程序框图如图，若输出的S值为九匹三丈（一匹=4丈，一丈=10尺），则框图中d为（ ）
《九章算术》之后，人们学会了用数列的知识来解决问题．公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为：“今有女善织，日益功疾，初日织五尺，今一月织九匹三丈．问日益几何？”．利用这种思想设计的一个程序框图如图，若输出的S值为九匹三丈（一匹=4丈，一丈=10尺），则框图中d为（ ）| A． | $\frac{1}{2}$尺 | B． | $\frac{8}{15}$尺 | C． | $\frac{16}{31}$尺 | D． | $\frac{16}{29}$尺 |
3．设a，b，c，d是四条不同的直线，且a，b为异面直线，命题p“c与a，b都相交，d与a，b都相交”，命题q“c，d为相交直线”，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
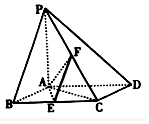如图，已知四棱锥P-ABCD，地面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．