题目内容

16．过三棱锥A-BCD的棱AB，BC，CD的中点M，N，P作平面MNP，三棱锥的六条棱中与平面MNP平行的是AC，BD．

分析 利用线面平行的性质定理求解．

解答 解：过三棱锥A-BCD的棱AB、BC、CD的中点M、N、P作平面MNP，
如图，MN∥AC，BD∥NP，
∵MN?平面MNP，AC?平面MNP，
∴AC∥平面MNP，同理BD∥平面MNP．
∴三棱锥的六条棱中与平面MNP平行的是AC，BD．
故答案为：AC，BD．

点评 本题考查三棱锥的六条棱中与平面MNP平行的棱的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
12．已知an=（$\frac{1}{3}$）n，把数列{an}的各项排成如图的三角形，记A（s，t）表示第s行的第t个数，则A（11，12）=（　　）
A．（$\frac{1}{3}$）67B．（$\frac{1}{3}$）68C．（$\frac{1}{3}$）112D．（$\frac{1}{3}$）113
7．已知F1，F2分别是椭圆的左、右焦点，现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M、N，若过F1的直线MF1是圆F2的切线，则椭圆的离心率为$\sqrt{3}$-1．
4．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为ρ=6sinθ．
（ I）求直角坐标下圆C的标准方程；
（Ⅱ）若点P（l，2），设圆C与直线l交于点A，B，求|PA|+|PB|的值．
11．设函数f（x）=x4+ax3+2x2+b（x∈R），其中a，b∈R．
（1）当a=-$\frac{10}{3}$时，讨论函数f（x）的单调性；
（2）若函数f（x）仅在x=0处有极值，求a的取值范围；
（3）若对于任意的a∈[-2，2]，不等式f（x）≤1在[-1，0]上恒成立，求b的取值范围．
1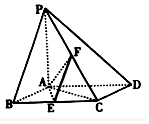．如图，已知四棱锥P-ABCD，地面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（1）证明：AE⊥PD；
（Ⅱ）若AB=2，PA=2，求四面体P-AEF的体积．
8．不论k为任何实数，直线（k+1）x-（k+2）y+k-3=0恒过定点（-5，-4）．
5．$\int_0^π{2{{sin}^2}}\frac{x}{2}$dx+$\int_0^1{\sqrt{1-{x^2}}}$dx=$\frac{5π}{4}$．
6．下列函数中，奇函数是（　　）
A．y=x2B．y=2xC．y=log2xD．y=2x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网