题目内容
6．下列说法正确的是（ ）| A． | 直线的倾斜角的取值范围是[0°，180°] | |
| B． | 若直线的倾斜角为90°，则这条直线与y轴平行 | |
| C． | 任意一条直线都有倾斜角和斜率 | |
| D． | 若直线l的倾斜角为锐角，则它的斜率大于0；若直线l的倾斜角为钝角，则它的斜率小于0 |
分析 A，直线的倾斜角的取值范围是[0°，180°）；
B，直线的倾斜角为90°，这条直线与y轴平行或重合；
C，直线都的倾斜角为900时无斜率；
D，当倾斜角θ≠900时，直线的斜率k=tanθ，由正切函数的性质可判定，
解答 解：对于A，直线的倾斜角的取值范围是[0°，180°），故错；
对于B，若直线的倾斜角为90°，则这条直线与y轴平行或重合，故错；
对于C，直线都的倾斜角为900时无斜率，故错；
对于D，当倾斜角θ≠900时，直线的斜率k=tanθ，由正切函数的性质可判定，直线l的倾斜角为锐角，
则它的斜率大于0；若直线l的倾斜角为钝角，则它的斜率小于0，故正确．
故选：D．
点评 本题考查了直线的倾斜角、斜率的定义及性质，属于基础题．
练习册系列答案
相关题目
2．
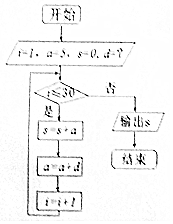《九章算术》之后，人们学会了用数列的知识来解决问题．公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为：“今有女善织，日益功疾，初日织五尺，今一月织九匹三丈．问日益几何？”．利用这种思想设计的一个程序框图如图，若输出的S值为九匹三丈（一匹=4丈，一丈=10尺），则框图中d为（ ）
《九章算术》之后，人们学会了用数列的知识来解决问题．公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为：“今有女善织，日益功疾，初日织五尺，今一月织九匹三丈．问日益几何？”．利用这种思想设计的一个程序框图如图，若输出的S值为九匹三丈（一匹=4丈，一丈=10尺），则框图中d为（ ）| A． | $\frac{1}{2}$尺 | B． | $\frac{8}{15}$尺 | C． | $\frac{16}{31}$尺 | D． | $\frac{16}{29}$尺 |
17．为了得到函数y=sin（2x-$\frac{π}{3}$）的图象，只需将函数y=sin2x的图象上所有的点（ ）
| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向左平移$\frac{π}{3}$个单位 | ||
| C． | 向右平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
14．已知f（x）=x2+2xf′（-1），则f′（0）等于（ ）
| A． | 4 | B． | 0 | C． | -2 | D． | 2 |
1．
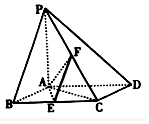如图，已知四棱锥P-ABCD，地面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（1）证明：AE⊥PD；
（Ⅱ）若AB=2，PA=2，求四面体P-AEF的体积．
如图，已知四棱锥P-ABCD，地面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．（1）证明：AE⊥PD；
（Ⅱ）若AB=2，PA=2，求四面体P-AEF的体积．
18．已知三棱锥P-ABC的四个顶点P，A，B，C都在半径为R的同一个球面上，若PA，PB，PC两两相互垂直，且PA=1，PB=2，PC=3，则R等于（ ）
| A． | $\frac{{\sqrt{14}}}{2}$ | B． | $\sqrt{14}$ | C． | $\frac{{\sqrt{13}}}{2}$ | D． | $\sqrt{3}$ |
15．已知向量$\overrightarrow a=（{m，1}），\overrightarrow b=（{1，n-2}），（{m＞0，n＞0}）$若$\overrightarrow a⊥\overrightarrow b$，则$\frac{1}{m}+\frac{2}{n}$的最小值为（ ）
| A． | 2$\sqrt{2}$ | B． | $\frac{3}{2}$+$\sqrt{2}$ | C． | 3$\sqrt{2}$+2 | D． | 2$\sqrt{2}$+3 |
16．
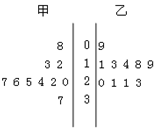某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图所示，则下列结论错误 的一个是（ ）
某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图所示，则下列结论错误 的一个是（ ）| A． | 甲的极差是29 | B． | 甲的中位数是25 | ||
| C． | 乙的众数是21 | D． | 甲的平均数比乙的大 |