题目内容
将八进制数131(8)化为二进制数为( )
| A、1011001(2) |
| B、1001101(2) |
| C、1000011(2) |
| D、1100001(2) |
考点:进位制,排序问题与算法的多样性
专题:函数的性质及应用
分析:进位制之间的转化一般要先化为十进制数,再化为其它进位制数,先将8进制数转化为十进制数,再由除K取余法转化为二进制数即可.
解答:
解:131(8)=1×80+3×81+1×82=89
89÷2=44…1,
44÷2=22…0,
22÷2=11…0,
11÷2=5…1,
5÷2=2…1,
2÷2=1…0,
1÷2=0…1,
∴89(10)=1011001(2).
故选A
89÷2=44…1,
44÷2=22…0,
22÷2=11…0,
11÷2=5…1,
5÷2=2…1,
2÷2=1…0,
1÷2=0…1,
∴89(10)=1011001(2).
故选A
点评:本题考查的知识点是十进制与其它进制之间的转化,其中熟练掌握“除k取余法”的方法步骤是解答本题的关键.属于基础题.

练习册系列答案
相关题目
如果直线ax+by=2与圆x2+y2=4相切,那么a+b的最大值为( )
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
下列函数中,最小正周期为π的偶函数为( )
A、y=sin(x+
| ||||
B、y=
| ||||
| C、y=2tan2x | ||||
| D、y=sinxcosx |
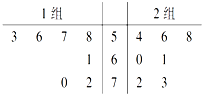 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
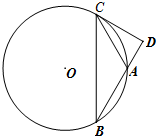 【几何证明选讲选做题】
【几何证明选讲选做题】 如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )


