题目内容
函数f(x)=log2(-x2+ax+3)在(1,2)是单调递减的,则a的取值范围是 .
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:由复合函数的单调性可知,y=-x2+ax+3在(1,2)是单调递减的且恒大于0,从而求解.
解答:
解:由复合函数的单调性可知,
y=-x2+ax+3在(1,2)是单调递减的且恒大于0,
则
,
解得,
≤a≤2,
故答案为:
≤a≤2.
y=-x2+ax+3在(1,2)是单调递减的且恒大于0,
则
|
解得,
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了复合函数的单调性的应用与二次函数及对数函数的性质,属于基础题.

练习册系列答案
相关题目
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=log2x,则f(-
)=( )
| 5 |
| 2 |
| A、0 | ||
B、
| ||
| C、1 | ||
D、
|
下列向量是单位向量的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果函数f(x)=x2-(a-1)x+3在区间(4,+∞)上是增函数,那么实数a的取值范围是( )
| A、(-∞,9] |
| B、[5,+∞) |
| C、[9,+∞) |
| D、(-∞,5] |
已知点(
,
)在幂函数y=f(x)的图象上,则f(x)的表达式是( )
| ||
| 3 |
| ||
| 9 |
A、f(x)=
| ||
| B、f(x)=x3 | ||
| C、f(x)=x-2 | ||
D、f(x)=(
|
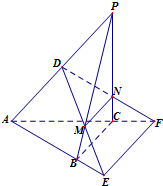 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F. 函数f(x)=Asin(2x+φ),(A>0,|φ|<
函数f(x)=Asin(2x+φ),(A>0,|φ|<