Question

记max{a，b}为两数a，b的最大值，当正数x，y变化时，t=max{

1

x

，

2

y

，4x²+y²}的最小值为（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

考点：函数的最值及其几何意义

专题：函数的性质及应用

分析：令y=kx，代入t=max{

1

x

，

2

y

，4x2+y2}，可得t=max{

1

x

，

2

k

•

1

x

，(4+k2)x2}，然后通过比较三个函数，得到t的最小值．

解答： 解：令y=kx（k＞0），代入t=max{

1

x

，

2

y

，4x2+y2}，可得t=max{

1

x

，

2

k

•

1

x

，(4+k2)x2}，
当

2

k

≥1，即0＜k≤2时，显然

2

k

•

1

x

≥

1

x

，做出y=

2 k

x

与y=（4+k²）x²的图象可知，t在交点处取得最小值．
令

2 k

x

=（4+k²）x²得x=

3	2 4k+k3

，代入y=

2 k

x

得y=

2

k

3	2 4k+k3

=

2

3 2 4 k2 +1

．易知当k=2时，得最小值为2；

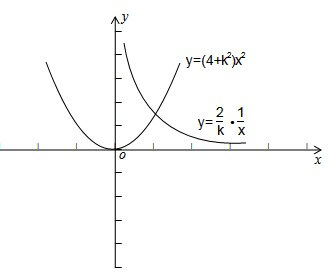
当

2

k

≤1即k≥2时，显然

1

x

≥

2

k

•

1

x

，做出y=

1

x

与y=（4+k²）x²的图象可知，t在交点处取得最小值．
令

1

x

=(4+k2)x2得x=

3	1 4+k2

，代入y=x得y=

1

x

=

3	4+k2

，当k=2时，得最小值为2．

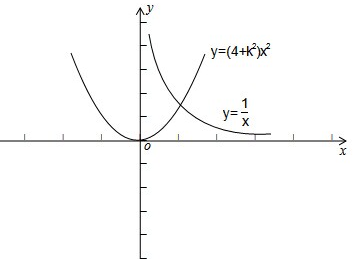
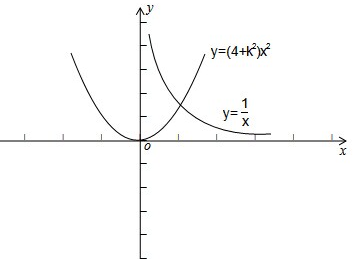
综上，t的最小值为2．

点评：这个题意思是清楚，就是求几个互相牵制的函数里的最大值中的最小值，可以猜出来x=

1

2

，y=1时最小，思路的话应该是用y=kx先统一成x的函数，最后讨论各种情况