题目内容
9.已知0<α<$\frac{π}{2}$,cos(2π-α)-sin(π-α)=-$\frac{\sqrt{5}}{5}$(1)求sinα+cosα的值;
(2)求$\frac{{{{cos}^2}(\frac{3π}{2}+α)+2cosαcos(\frac{π}{2}-α)}}{{1+{{sin}^2}(\frac{π}{2}-α)}}$的值.
分析 (1)原式化简,利用二倍角的正弦函数公式可求${({cosα+sinα})^2}=\frac{9}{5}$,结合范围0<α<$\frac{π}{2}$,即可得解sinα+cosα的值.
(2)由(1)即可解得cosα,sinα的值,利用诱导公式化简所求即可计算得解.
解答 解:(1)原式化简:$cosα-sinα=-\frac{{\sqrt{5}}}{5}$,
平方得:$1-2cosαsinα=\frac{1}{5}$$⇒2cosαsinα=\frac{4}{5}$$⇒1+2cosαsinα=\frac{9}{5}$,
因为:0<α<$\frac{π}{2}$,
所以:cosα+sinα>0
因为:${({cosα+sinα})^2}=\frac{9}{5}$,
所以:$cosα+sinα=\frac{{3\sqrt{5}}}{5}$.
(2)∵由$cosα-sinα=-\frac{{\sqrt{5}}}{5}$,$cosα+sinα=\frac{{3\sqrt{5}}}{5}$,
可得:cosα=$\frac{\sqrt{5}}{5}$,sinα=$\frac{2\sqrt{5}}{5}$,
∴原式化简得$\frac{{{{sin}^2}α+2cosαsinα}}{{1+{{cos}^2}α}}=\frac{4}{3}$.
点评 本题主要考查了诱导公式,二倍角的正弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
17.为了得到函数y=4cos2x的图象,只需将函数$y=4cos(2x+\frac{π}{4})$的图象上每一个点( )
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
1.若函数f(x)满足f(3x+2)=9x+8,则f(x)的解析式是( )
| A. | f(x)=9x+8 | B. | f(x)=3x+2 | ||
| C. | f(x)=-3x-4 | D. | f(x)=3x+2或f(x)=-3x-4 |
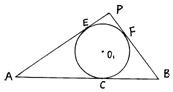 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
 如图所示,AC=BC=1,∠ACB-90°,PA⊥平面ABC,CE∥PA,PA=2CE=2,
如图所示,AC=BC=1,∠ACB-90°,PA⊥平面ABC,CE∥PA,PA=2CE=2,