题目内容
7.已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上一点,F1,F2为双曲线的左、右焦点,使($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0(O为坐标原点),且|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,则双曲线离心率为( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\sqrt{6}$+1 | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
分析 根据双曲线的定义可知和|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,可得|PF2|=($\sqrt{3}$+1)a,再根据($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0,得到△OPF2为等边三角形,即可得到c=($\sqrt{3}$+1)a,即可求出离心率.
解答 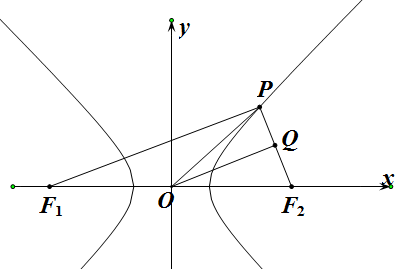 解:|PF1|-|PF2|=2a,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,
解:|PF1|-|PF2|=2a,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{P{F}_{2}}$|,
∴|PF2|=($\sqrt{3}$+1)a,
∵($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)($\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$)=0,
∴|$\overrightarrow{OP}$|=|$\overrightarrow{O{F}_{2}}$|,
设Q为PF2的中点,
∴$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$=2$\overrightarrow{OQ}$,$\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$=$\overrightarrow{{F}_{2}P}$,
∴$\overrightarrow{OQ}$⊥$\overrightarrow{{F}_{2}P}$,
∴△OPF2为等边三角形,
∴c=($\sqrt{3}$+1)a,
∴e=$\frac{c}{a}$=$\sqrt{3}$+1,
故选:C.
点评 本题考查双曲线的定义、方程和性质,考查直径所对的圆周角为直角,以及等腰三角形的性质,考查离心率公式的运用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (-∞,-1) | D. | (-∞,-1]∪[2,+∞) |
| A. | {0}⊆M | B. | M=∅ | C. | -1∈M | D. | 2∈M |
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
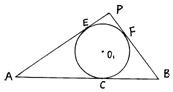 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.