题目内容
2.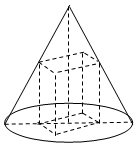 底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).(1)设正四棱柱的底面边长为x,试将棱柱的高h表示成x的函数;
(2)当x取何值时,此正四棱柱的表面积最大,并求出最大值.
分析 (1)根据比例关系式求出h关于x的解析式即可;(2)设该正四棱柱的表面积为y,得到关系式y=2x2+4xh,根据二次函数的性质求出y的最大值即可.
解答 解:(1)根据相似性可得:$\frac{{\frac{{\sqrt{2}}}{2}x}}{4}=\frac{{8\sqrt{2}-h}}{{8\sqrt{2}}}$…(3分)
解得:$h=8\sqrt{2}-2x(0<x<4\sqrt{2})$…(6分)(没范围扣1分)
(2)设该正四棱柱的表面积为y.则有关系式y=2x2+4xh
=$2{x^2}+4x(8\sqrt{2}-2x)$
=$-6{x^2}+32\sqrt{2}x$
=$-6{(x-\frac{8}{3}\sqrt{2})^2}+\frac{256}{3}$…(9分)
因为$0<x<4\sqrt{2}$,所以当$x=\frac{8}{3}\sqrt{2}$时,${y_{max}}=\frac{256}{3}$…(11分)
故当正四棱柱的底面边长为$\frac{8}{3}\sqrt{2}$时,此正四棱柱的表面积最大值为$\frac{256}{3}$…(12分)
点评 本题考查了数形结合思想,考查二次函数的性质以及求函数的最值问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.为了得到函数y=4cos2x的图象,只需将函数$y=4cos(2x+\frac{π}{4})$的图象上每一个点( )
| A. | 横坐标向左平动$\frac{π}{4}$个单位长度 | B. | 横坐标向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 横坐标向左平移$\frac{π}{8}$个单位长度 | D. | 横坐标向右平移$\frac{π}{8}$个单位长度 |
7.已知两条不同的直线m,n和平面α,下列说法正确的是( )
| A. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n∥α | |
| B. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n与α相交 | |
| C. | 如果m∥α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m?α,n∥α,m、n共面,那么m∥n |