题目内容
 已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x(1)求函数f(x)的解析式;
(2)画出函数f(x)的大致图象,并写出函数的单调增区间与单调减函数.
考点:函数奇偶性的性质,分段函数的应用
专题:函数的性质及应用
分析:(1)设0<x≤5,得-5≤-x<0,代入已知函数解析式结合偶函数的性质得答案;
(2)直接画出图象,由图象得到函数的单调期间.
(2)直接画出图象,由图象得到函数的单调期间.
解答:
解:(1)当0<x≤5时,-5≤-x<0,
∵函数为偶函数,故f(-x)=f(x),
∴f(x)=f(-x)=(-x)2+4(-x)=x2-4x.
∴f(x)=
;
(2)函数图象如图,
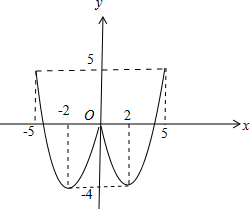
函数的得到增区间为[-2,0],[2,5];得到减区间为[-5,-2],[0,2].
∵函数为偶函数,故f(-x)=f(x),
∴f(x)=f(-x)=(-x)2+4(-x)=x2-4x.
∴f(x)=
|
(2)函数图象如图,
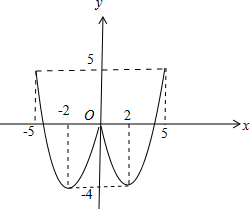
函数的得到增区间为[-2,0],[2,5];得到减区间为[-5,-2],[0,2].
点评:本题考查了函数奇偶性的性质,考查了函数解析式的求法,考查了分段函数的单调性,是中档题.

练习册系列答案
相关题目
已知两条直线l1:kx+(1-k)y-3=0和l2:(k-1)x+2y-2=0互相垂直,则k=( )
| A、1或-2 | B、-1或2 |
| C、1或2 | D、-1或-2 |
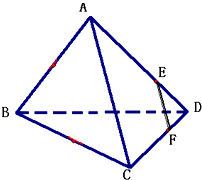 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明: