题目内容
已知向量
1,
2是两个不共线的向量,若
=2
1-
2与
=
1+λ
2共线,则λ= .
| e |
| e |
| a |
| e |
| e |
| b |
| e |
| e |
考点:平行向量与共线向量
专题:平面向量及应用
分析:由向量
1,
2是两个不共线的向量,以
、
为基底,把
、
用坐标表示,利用共线的定义,求出λ的值.
| e |
| e |
| e1 |
| e2 |
| a |
| b |
解答:
解:∵向量
1,
2是两个不共线的向量,不妨以
、
为基底,
则
=2
1-
2=(2,-1),
=
1+λ
2=(1,λ);
又∵
、
共线,
∴2λ-(-1)×1=0;
解得λ=-
.
故答案为:-
.
| e |
| e |
| e1 |
| e2 |
则
| a |
| e |
| e |
| b |
| e |
| e |
又∵
| a |
| b |
∴2λ-(-1)×1=0;
解得λ=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了平面向量的应用问题,解题时应利用平面向量的坐标表示进行解答,是基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增加的,又f(3)=0,则不等式
<0的解集为( )
| f(x)-f(-x) |
| x |
| A、(-3,0)∪(3,+∞) |
| B、(-3,0)∪(0,3) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
已知两条直线l1:kx+(1-k)y-3=0和l2:(k-1)x+2y-2=0互相垂直,则k=( )
| A、1或-2 | B、-1或2 |
| C、1或2 | D、-1或-2 |
 已知函数f(x)=ax2+(a-1)x+b的最小值为-1,且f(0)=-1.
已知函数f(x)=ax2+(a-1)x+b的最小值为-1,且f(0)=-1.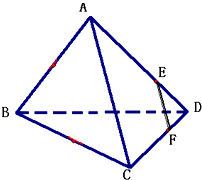 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明: