题目内容
奇函数f(x)=
的定义域为R,其中y=g(x)为指数函数且过点(2,4).
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若对任意的t∈[0,5],不等式f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,求实数k的取值范围.
| m-g(x) |
| 1+g(x) |
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若对任意的t∈[0,5],不等式f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,求实数k的取值范围.
考点:指数函数综合题,函数奇偶性的性质
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)设g(x)=ax(a>0,a≠1),代入点,即可得到g(x),再由奇函数的定义,即可得到m=1;
(Ⅱ)先判断f(x)的单调性,可运用导数或分离变量法,要使对任意的t∈[0,5],f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,即对任意的t∈[0,5],f(t2+2t+k)>-f(-2t2+2t-5)解集非空.再由奇函数和单调性的性质,运用分离参数方法,结合二次函数的最值,即可得到k的范围.
(Ⅱ)先判断f(x)的单调性,可运用导数或分离变量法,要使对任意的t∈[0,5],f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,即对任意的t∈[0,5],f(t2+2t+k)>-f(-2t2+2t-5)解集非空.再由奇函数和单调性的性质,运用分离参数方法,结合二次函数的最值,即可得到k的范围.
解答:
解:(Ⅰ)设g(x)=ax(a>0,a≠1),
则a2=4,∴a=2,
∴g(x)=2x,f(x)=
.
又∵f(x)为奇函数,
∴f(-x)=-f(x),∴
=-
,
整理得m(2x+1)=2x+1,∴m=1,
∴f(x)=
;
(Ⅱ)∵f′(x)=
<0,∴y=f(x)在R上单调递减.
也可用f(x)=
-1为R上单调递减.
要使对任意的t∈[0,5],f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,
即对任意的t∈[0,5],f(t2+2t+k)>-f(-2t2+2t-5)解集非空.
∵f(x)为奇函数,∴f(t2+2t+k)>f(2t2-2t+5)解集非空,
又∵y=f(x)在R上单调递减,∴t2+2t+k<2t2-2t+5,
当t∈[0,5]时有实数解,
∴k<t2-4t+5=(t-2)2+1当t∈[0,5]时有实数解,
而当t∈[0,5]时,1≤(t-2)2+1≤10,
∴k<10.
则a2=4,∴a=2,
∴g(x)=2x,f(x)=
| m-2x |
| 1+2x |
又∵f(x)为奇函数,
∴f(-x)=-f(x),∴
| m-2-x |
| 1+2-x |
| m-2x |
| 1+2x |
整理得m(2x+1)=2x+1,∴m=1,
∴f(x)=
| 1-2x |
| 1+2x |
(Ⅱ)∵f′(x)=
| -2.2xln2 |
| (1+2x)2 |
也可用f(x)=
| 2 |
| 1+2x |
要使对任意的t∈[0,5],f(t2+2t+k)+f(-2t2+2t-5)>0解集非空,
即对任意的t∈[0,5],f(t2+2t+k)>-f(-2t2+2t-5)解集非空.
∵f(x)为奇函数,∴f(t2+2t+k)>f(2t2-2t+5)解集非空,
又∵y=f(x)在R上单调递减,∴t2+2t+k<2t2-2t+5,
当t∈[0,5]时有实数解,
∴k<t2-4t+5=(t-2)2+1当t∈[0,5]时有实数解,
而当t∈[0,5]时,1≤(t-2)2+1≤10,
∴k<10.
点评:本题考查函数的奇偶性和单调性及运用:求函数的表达式和解不等式,考查运算能力,考查分离参数的方法,属于中档题和易错题.

练习册系列答案
相关题目
设函数f(x)=
,若f(a)=1,则实数a的值为( )
|
| A、-1或0 | B、2或-1 |
| C、0或2 | D、2 |
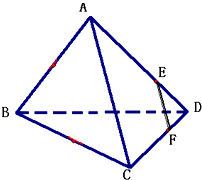 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明: