题目内容
12.过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB中点的纵坐标为6,则抛物线的方程为( )| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
分析 设过点M的抛物线的切线方程与抛物线的方程联立,利用方程的判别式等于0,再利用韦达定理,结合线段AB中点的纵坐标为6,可求抛物线的方程.
解答 解:设过点M的抛物线的切线方程为:y+2p=k(x-2)与抛物线的方程联立消y得:x2-2pkx+4pk+4p2=0
此方程的判别式等于0,∴pk2-4k-4p=0
设切线的斜率分别为k1,k2,则k1+k2=$\frac{4}{p}$,
此时x=pk,∴y=$\frac{{x}^{2}}{2p}$=2(k+p),
设A(x1,y1),B(x2,y2),则12=y1+y2=2(k1+k2)+4p=$\frac{8}{p}$+4p,
∴p2-3p+2=0,
∴p=1或p=2,
∴所求抛物线的方程为x2=2y或x2=4y,
故选C.
点评 本题考查抛物线的切线,考查韦达定理的运用,考查中点坐标公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足$\overrightarrow{FA}$•$\overrightarrow{FB}$=0,若|FA|=|FB|,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}-1$ | D. | $\frac{\sqrt{3}}{2}$ |
2.三角形的面积为S=$\frac{1}{2}$(a+b+c)•r,(a,b,c为三角形的边长,r为三角形的内切圆的半径)利用类比推理,可以得出四面体的体积为( )
| A. | V=$\frac{1}{3}$abc(a,b,c,为底面边长) | |
| B. | V=$\frac{1}{3}$Sh(S为底面面积,h为四面体的高) | |
| C. | V=$\frac{1}{3}$(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面 体内切球的半径) | |
| D. | V=$\frac{1}{3}$(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高) |
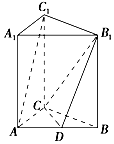 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.