题目内容
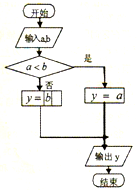定义某种运算※，a※b的运算原理如图所示，设f（x）=（0※x）x-（2※x），则f（x）在区间[-2，2]上的最小值为（ ）| A、-2 | B、-4 | C、-6 | D、0 |
考点：程序框图
专题：函数的性质及应用,算法和程序框图
分析：通过程序框图判断出a※b的解析式，再求出f（x）的解析式，从而求出f（x）的解析式，最后令x=-2即可得到函数的最小值．
解答：
解：由已知中的流程图可得a※b=
，
∴f（x））=（0※x）x-（2※x）=
=
，
又∵x∈[-2，2]，
∴当x=-2时，f（x）取最小值-6，
故选：C
|
∴f（x））=（0※x）x-（2※x）=
|
|
又∵x∈[-2，2]，
∴当x=-2时，f（x）取最小值-6，
故选：C
点评：本题考查选择结构，主要考查了判断程序框图的功能即判断出新运算法则，利用运算法则求值．解决新定义题关键是理解题中给的新定义．
练习册系列答案
相关题目
不等式|x|＞
的解集是（ ）
| 1 |
| x |
| A、（-∞，-1）∪（1，+∞） |
| B、（-∞，0）∪（1，+∞） |
| C、（-1，0）∪（1，+∞） |
| D、（-∞，-1）∪（0，1） |
函数f（x）=
的图象大致是（ ）
| x3-3 |
| ex |
A、 |
B、 |
C、 |
D、 |
椭圆的焦点为F1，F2，过F1的最短弦PQ的长为10，△PF2Q的周长为36，则此椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC的内角A、B、C的对边分别为a、b、c，若a2-c2=b2+bc，则A=（ ）
| A、30° | B、60° |
| C、120° | D、150° |
已知x，y之间的数据如表所示，则回归直线过点（ ）
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1.2 | 1.8 | 2.5 | 3.2 | 3.8 |
| A、（0，0） |
| B、（2，1.8） |
| C、（3，2.5） |
| D、（4，3.2） |
