题目内容
已知函数f(x)=2lnx-x2.
(1)求函数f(x)在[
,2]的最大值;
(2)求证:
2n•ln(1+2-n)<n+
(n∈N*);
(3)函数h(x)=f(x)-mx的图象与x轴交于A(x1,0),B(x2,0),且0<x1<x2,若正常数α,β满足α+β=1,β≥α.求证:h′(αx1+βx2)<0.
(1)求函数f(x)在[
| 1 |
| 2 |
(2)求证:
| n |
 |
| k=1 |
| 1 |
| 2 |
(3)函数h(x)=f(x)-mx的图象与x轴交于A(x1,0),B(x2,0),且0<x1<x2,若正常数α,β满足α+β=1,β≥α.求证:h′(αx1+βx2)<0.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由f′(x)=
-2x=
,能求出函数f(x)在[
,2]的最大值.
(2)由(1)知2lnx<x2-1,令x=1+2-n,得2nln(1+2-n)<1+2-n-1.由此能证明
2n•ln(1+2-n)<n+
(n∈N*).
(3)由题意知h′(x)=
-m,m=
-(x1+x2),从而得到
+lnt<0,只证u(t)=lnt+
<0即可,由此能证明h′(αx1+βx2)<0.
| 2 |
| x |
| 2-2x2 |
| x |
| 1 |
| 2 |
(2)由(1)知2lnx<x2-1,令x=1+2-n,得2nln(1+2-n)<1+2-n-1.由此能证明
| n |
 |
| k=1 |
| 1 |
| 2 |
(3)由题意知h′(x)=
| 2 |
| x |
| 2(lnx1-lnx2) |
| x1-x2 |
| 1-t |
| αt+β |
| 1-t |
| αt+β |
解答:
(1)解:∵f(x)=2lnx-x2,∴f′(x)=
-2x=
,
由f′(x)=0,得x=1,或x=-1(舍).
列表讨论:
∴函数f(x)在[
,2]的最大值为f(1)=-1.
(2)证明:由(1)知2lnx-x2<-1,
∴2lnx<x2-1,令x=1+2-n,
∴2ln(1+2-n)<(1+2-n)2-1=2•2-n+2-2n,
∴2nln(1+2-n)<1+2-n-1.
(3)证明:∵h(x)=f(x)-mx,
∴h′(x)=
-m,又f(x)-mx=0有两个实根x1,x2,
∴
,
两式相减,得2(lnx1-lnx2)-(x12-x22)=m(x1-x2),
∴m=
-(x1+x2),
∴h′(αx1+βx2)=
-2(αx1+βx2)-
+(x1+x2)
=
-
+(2α-1)(x1-x2),
,∴2α≤1,∴(2α-1)(x2-x1)≤0,
∴
+lnt<0,只证u(t)=lnt+
<0即可,
μ′(t)=
+
=
-
=
=
.
∵μ(t)<μ(1)=0,∴lnt+
<0,
即
+ln
<0,
∴h′(αx1+βx2)<0.
| 2 |
| x |
| 2-2x2 |
| x |
由f′(x)=0,得x=1,或x=-1(舍).
列表讨论:
| x | (0,1) | 1 | (1,+∞) |
| f’(x) | + | 0 | - |
| f(x) | ↑ | 极大值 | ↑ |
| 1 |
| 2 |
(2)证明:由(1)知2lnx-x2<-1,
∴2lnx<x2-1,令x=1+2-n,
∴2ln(1+2-n)<(1+2-n)2-1=2•2-n+2-2n,
∴2nln(1+2-n)<1+2-n-1.
|
(3)证明:∵h(x)=f(x)-mx,
∴h′(x)=
| 2 |
| x |
∴
|
两式相减,得2(lnx1-lnx2)-(x12-x22)=m(x1-x2),
∴m=
| 2(lnx1-lnx2) |
| x1-x2 |
∴h′(αx1+βx2)=
| 2 |
| αx1+βx2 |
| 2(lnx1-lnx2) |
| x1-x2 |
=
| 2 |
| αx1+βx2 |
| 2(lnx1-lnx2) |
| x1-x2 |
|
∴
| 1-t |
| αt+β |
| 1-t |
| αt+β |
μ′(t)=
| 1 |
| t |
| -(αt+β)-(1-t)α |
| (αt+β)2 |
| 1 |
| t |
| 1 |
| (αt+β)2 |
| (αt+β)2-t |
| t(αt+β)2 |
α2(t-1)(t-
| ||
| t(αt+β)2 |
∵μ(t)<μ(1)=0,∴lnt+
| 1-t |
| αt+β |
即
| x1-x2 |
| αt+β |
| x1 |
| x2 |
∴h′(αx1+βx2)<0.
点评:本题考查函数最大值的求法,考查不等式的证明,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
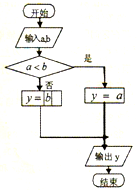 定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )
定义某种运算※,a※b的运算原理如图所示,设f(x)=(0※x)x-(2※x),则f(x)在区间[-2,2]上的最小值为( )| A、-2 | B、-4 | C、-6 | D、0 |
已知cosα=-
,sinα=
,那么α的终边所在的象限为( )
| 3 |
| 5 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |