题目内容
如图所示是函数f（x）的导函数f′（x）的图象，则下列判断中正确的是（ ）
| A、函数f（x）在区间（-2，0）上是减函数 |
| B、函数f（x）在区间（1，3）上是减函数 |
| C、函数f（x）在区间（0，2）上是减函数 |
| D、函数f（x）在区间（3，4）上是增函数 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：通过读图得到函数f（x）的导数的取值范围，进而求出函数f（x）的单调区间，从而得到答案．
解答：
解；由题意得：
在区间（-2，0），和（2，4）上，f′x）＜0，∴f（x）是减函数，
在区间（0，2）上，f′（x）＞0，∴f（x）是增函数，
故选：A．
在区间（-2，0），和（2，4）上，f′x）＜0，∴f（x）是减函数，
在区间（0，2）上，f′（x）＞0，∴f（x）是增函数，
故选：A．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
若角α的终边落在直线x+y=0上，则
+
的值等于（ ）
| |tanα| |
| tanα |
| sinα | ||||
|
| A、2或-2或0 | B、-2或0 |
| C、2或-2 | D、0或2 |
下列判断正确的是（ ）
A、若向量
| ||||
| B、单位向量都相等 | ||||
| C、共线的向量，若起点不同，则终点一定不同 | ||||
| D、模为0的向量的方向是不确定的 |
已知双曲线
-
=1的一条渐近线方程为4x+3y=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
cos
的值是（ ）
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
如图所示是《函数的应用》的知识结构图，如果要加入“用二分法求方程的近似解”，则应该放在（ ）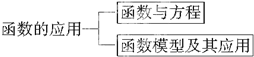
| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=4，AD=2，PA=2，PD=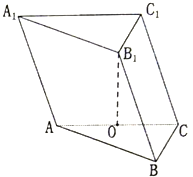
已知三棱柱ABC-A1B1C1的各条棱长均为2，点B1在平面ABC内的射影恰好落在AC边的中点O处．