题目内容
已知函数f(x)=x+
,(x>0,a>0).
(1)当a=4时,求函数f(x)的最小值;
(2)若函数f(x)>-x+4,求实数a的取值范围.
| a |
| x |
(1)当a=4时,求函数f(x)的最小值;
(2)若函数f(x)>-x+4,求实数a的取值范围.
考点:基本不等式,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)a=4时,f(x)=x+
≥2
=4,求出f(x)的最小值;
(2)由f(x)>-x+4,得出a>-2x2+4x;求出y=-2x2+4x的最大值,即得实数a的取值范围.
| 4 |
| x |
x•
|
(2)由f(x)>-x+4,得出a>-2x2+4x;求出y=-2x2+4x的最大值,即得实数a的取值范围.
解答:
解:(1)当a=4时,f(x)=x+
,
∵x>0,
∴f(x)=x+
≥2
=4,
当且仅当x=2时“=”成立;
∴f(x)的最小值为4;
(2)∵f(x)>-x+4,
即x+
>-x+4;
又x>0,
∴a>-2x2+4x;
令y=-2x2+4x(x>0),
∴y=-2(x-1)2+2,
当x=1时,y取得最大值2,
∴a>2;
即实数a的取值范围是{a|a>2}.
| 4 |
| x |
∵x>0,
∴f(x)=x+
| 4 |
| x |
x•
|
当且仅当x=2时“=”成立;
∴f(x)的最小值为4;
(2)∵f(x)>-x+4,
即x+
| a |
| x |
又x>0,
∴a>-2x2+4x;
令y=-2x2+4x(x>0),
∴y=-2(x-1)2+2,
当x=1时,y取得最大值2,
∴a>2;
即实数a的取值范围是{a|a>2}.
点评:本题考查了函数的性质及其应用问题,解题时应根据函数解析式的特点,利用基本不等式求函数的最值,利用配方法求函数的最值,是基础题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
有以下四种变换方式:
①向左平移
个单位长度,再将每个点的横坐标缩短为原来的
;
②向右平移
个单位长度,再将每个点的横坐标缩短为原来的
;
③每个点的横坐标缩短为原来的
,向右平移
个单位长度;
④每个点的横坐标缩短为原来的
,向左平移
个单位长度;
其中能将y=sinx的图象变换成函数y=sin(2x+
)的图象的是( )
①向左平移
| π |
| 4 |
| 1 |
| 2 |
②向右平移
| π |
| 8 |
| 1 |
| 2 |
③每个点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
④每个点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
其中能将y=sinx的图象变换成函数y=sin(2x+
| π |
| 4 |
| A、①和③ | B、①和④ |
| C、②和④ | D、②和③ |
cos
的值是( )
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=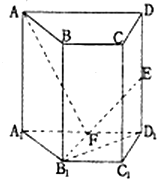 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.