题目内容
已知函数f(x)=
,则函数y=f|f(x)|-1的零点个数是( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:根的存在性及根的个数判断,函数的零点与方程根的关系
专题:计算题,作图题,函数的性质及应用
分析:由题意作函数f(x)=
的图象,由图象及复合函数的性质求解零点的个数.
|
解答:
解:作函数f(x)=
的图象如下,
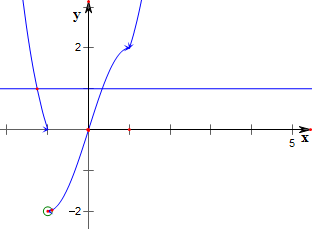
令y=f(f(x))-1=0,
则f(f(x))=1,由图知,
f(x)有两个值,一个值在(-2,-1)上,另一个值在(0,1)上,
由图知,f(x)在(-2,-1)上时有一个x值,
f(x)在(0,1)上时有两个x值,
故共有3个值,
故选C.
|

令y=f(f(x))-1=0,
则f(f(x))=1,由图知,
f(x)有两个值,一个值在(-2,-1)上,另一个值在(0,1)上,
由图知,f(x)在(-2,-1)上时有一个x值,
f(x)在(0,1)上时有两个x值,
故共有3个值,
故选C.
点评:本题考查了复合函数的应用及函数的零点的应用,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
若函数f(x)=5sin(ωx+
)(ω>0)与g(x)=2sin(2x+φ)(0<φ<π)的图象有相同的对称轴,则函数g(x)的一个单调区间为( )
| π |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[π,
|
已知在△ABC中,若∠C=90°,则三边的比
=( )
| a+b |
| c |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若如图所给程序框图运行的结果恰为s>
,那么判断框中可以填入的关于k的判断条件是( )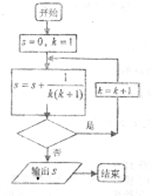
| 2012 |
| 2013 |

| A、k>2013 |
| B、k>2012 |
| C、k<2013 |
| D、k<2012 |
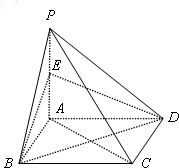 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.