题目内容
已知在△ABC中，若∠C=90°，则三边的比
=（ ）
| a+b |
| c |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：正弦定理
专题：解三角形
分析：由正弦定理以及和差化积公式可得
=
=sinA+sinB=2sin
cos
，代值化简可得．
| a+b |
| c |
| sinA+sinB |
| sinC |
| A+B |
| 2 |
| A-B |
| 2 |
解答：
解：∵在△ABC中，∠C=90°，
∴由正弦定理可得
=
=sinA+sinB，
由和差化积公式可得sinA+sinB=2sin
cos
=2sin45°cos
=
cos
故选：B
∴由正弦定理可得
| a+b |
| c |
| sinA+sinB |
| sinC |
由和差化积公式可得sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
=2sin45°cos
| A-B |
| 2 |
| 2 |
| A-B |
| 2 |
故选：B
点评：本题考查正弦定理以及和差化积公式，属基础题．
练习册系列答案
相关题目
在平面直角坐标系xOy中设锐角α的始边与x轴的非负半轴重合，终边与单位圆交于点P（x1，y1），将射线OP绕坐标原点O按逆时针方向旋转
已知函数y=
的单调增区间是（ ）
| -x2+4x+5 |
| A、（-∞，2] |
| B、[-1，2] |
| C、[2，+∞] |
| D、[2，5] |
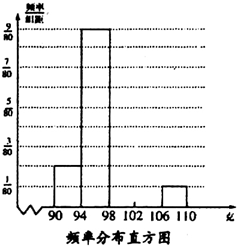为了解食品厂生产的一种食品中添加剂的含量，食品监管部门随机抽取了一个批次的20袋样品进行检验，获得以下频率分布表和频率分布直方图：