题目内容
在△ABC中,角A、B、C依次成等差数列,其对边依次分别为a,b,c.
(Ⅰ)若cos(B+C)=-
,求cosC的值;
(Ⅱ)若a=3,
•
=3,求b.
(Ⅰ)若cos(B+C)=-
| ||
| 3 |
(Ⅱ)若a=3,
| AC |
| CB |
考点:平面向量数量积的运算,余弦定理
专题:平面向量及应用
分析:(1)由题意可得B=60°,由cos(B+C)=-
,可得得sin(B+C)的值,而cosC=cos[(B+C)-B]=cos(B+C) cosB+sin(B+C) sinB,代入数值计算可得;(2)由
•
=3可得abcosC=-3,结合a=3,可得bcosC=-1,①,再由正弦定理可得bsinC=4
,③,联立①③可解.
| ||
| 3 |
| AC |
| CB |
| 3 |
解答:
解:(1)∵在△ABC中,因为角A、B、C依次成等差数列,∴2B=A+C
又∵A+B+C=180°,∴B=60°,
由cos(B+C)=-
,得sin(B+C)=
=
,
∴cosC=cos[(B+C)-B]=cos(B+C) cosB+sin(B+C) sinB
=-
×
+
×
=
.
(2)由
•
=3得|
|||
|cos(180°-C)=3,即abcosC=-3,
又a=3,∴bcosC=-1,①
由正弦定理
=
得
=
,
∴
bcosC+bsinC=3
,②
将①代入②得bsinC=4
,③
联立①③可解得b=7
又∵A+B+C=180°,∴B=60°,
由cos(B+C)=-
| ||
| 3 |
| 1-cos2(B+C) |
| ||
| 3 |
∴cosC=cos[(B+C)-B]=cos(B+C) cosB+sin(B+C) sinB
=-
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
3-
| ||
| 6 |
(2)由
| AC |
| CB |
| AC |
| CB |
又a=3,∴bcosC=-1,①
由正弦定理
| a |
| sinA |
| b |
| sinB |
| a |
| sin(120°-C) |
| b |
| sin60° |
∴
| 3 |
| 3 |
将①代入②得bsinC=4
| 3 |
联立①③可解得b=7
点评:本题考查平面向量数量积的运算,涉及三角形的正余弦定理,属中档题.

练习册系列答案
相关题目
如图所示的圆锥的俯视图为( )


A、 |
B、 |
C、 |
D、 |
若复数z=
对应的点在直线x+2y+5=0上,则实数a的值为( )
| 1-ai |
| i |
| A、1 | B、2 | C、3 | D、4 |
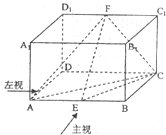 长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )
长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( ) 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表: