Question

为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表：

月工资 （单位：百元）	[15，25）	[25，35）	[35，45）	[45，55）	[55，65）	[65，75）
男员工数	1	8	10	6	4	4
女员工数	4	2	5	4	1	1

（Ⅰ）完成如图月工资频率分布直方图（注意填写纵坐标）；
（Ⅱ）试由图估计该单位员工月平均工资；
（Ⅲ）若从月工资在[25，35）和[45，55）两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．

Answer 1

考点：古典概型及其概率计算公式,频率分布直方图

专题：概率与统计

分析：（Ⅰ）根据题意，分析可得各组的频率，计算可得图中各组的纵坐标，即可得频率分布直方图；
（Ⅱ）该单位员工月平均工资为各小矩形的面积与相应的底边中点的横坐标乘积之和；
（Ⅲ）计算从6名女员工中随机抽取2名的抽法种数，再计算这2人月工资差不超过1000元的抽法种数，利用古典概型概率公式计算．

解答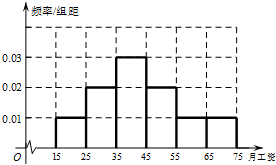： 解：（Ⅰ）如图
（Ⅱ） 20×0.1+30×0.2+40×0.3+50×0.2+60×0.1+70×0.1=43（百元）
即该单位员工月平均工资估计为4300元．
（Ⅲ）由上表可知：月工资在[25，35）组的有两名女工，分别记作甲和乙；
月工资在[45，55）组的有四名女工，分别记作A，B，C，D．
现在从这6人中随机选取2人的基本事件有如下15组：
（甲，乙），（甲，A），（甲，B），（甲，C），（甲，D），
（乙，A），（乙，B），（乙，C），（乙，D），
（A，B），（A，C），（A，D），
（B，C），（B，D），
（C，D）
其中月工资差不超过1000元，
即为同一组的有（甲，乙），（A，B），（A，C），（A，D），（B，C），（B，D），（C，D）共7组，
∴所求概率为P=

7

15

．

点评：本题考查频率分布直方图、样本特征数、古典概型，简单题．