题目内容
已知直线l：y=kx与圆C1：（x-1）2+y2=1相交于A、B两点，圆C2与圆C1相外切，且与直线l相切于点M（3，
），求
（1）k的值
（2）|AB|的值
（3）圆C2的方程．
| 3 |
（1）k的值
（2）|AB|的值
（3）圆C2的方程．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）点M在直线上，即可求出k的值；
（2）求出圆心到直线有距离，即可求出|AB|；
（3）利用圆C1与圆C2相切，可得
=1+2|m-3|，分类讨论，即可求出圆C2的方程．
（2）求出圆心到直线有距离，即可求出|AB|；
（3）利用圆C1与圆C2相切，可得
| (m-3)2+3(m-4)2 |
解答：
解：（1）由题意知，点M在直线上，所以k=
（2分）
（2）圆心到直线有距离d=
=
，于是|AB|=2
=
（4分）
（3）设所求的圆心的坐标为C2（m，n），半径为R．
由题意知C2M⊥l，则kC2M•kl=-1，即n=-
m+4
，从而R=C2M=2|m-3|，（8分）
又圆C1与圆C2相切，则C1C2=
=1+R，
即：
=1+2|m-3|
（A）当m≥3时解得：m=4，n=0，R=2，则圆C2的方程为：（x-4）2+y2=4
（B）当m，3时解得：m=0，n=4
，R=6，则圆C2的方程为：x2+(y-4
)2=36
所以所求圆的方程为：（x-4）2+y2=4，x2+(y-4
)2=36（14分）
| ||
| 3 |
（2）圆心到直线有距离d=
|1-
| ||||
|
| 1 |
| 2 |
| r2-d2 |
| 3 |
（3）设所求的圆心的坐标为C2（m，n），半径为R．
由题意知C2M⊥l，则kC2M•kl=-1，即n=-
| 3 |
| 3 |
又圆C1与圆C2相切，则C1C2=
| (m-1)2+n2 |
即：
| (m-3)2+3(m-4)2 |
（A）当m≥3时解得：m=4，n=0，R=2，则圆C2的方程为：（x-4）2+y2=4
（B）当m，3时解得：m=0，n=4
| 3 |
| 3 |
所以所求圆的方程为：（x-4）2+y2=4，x2+(y-4
| 3 |
点评：本题考查直线和圆的方程的应用，考查点到直线的距离公式，考查分类讨论的数学思想，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
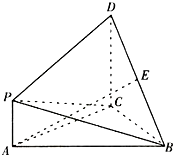如图，△ABC是等边三角形，PA⊥平面ABC，DC∥PA，且DC=AC=2PA=2，E是BD的中点．