题目内容
设
=(cosx,sinx),
=(cosx,
cosx),f(x)=
•
,x∈R.
(1)求f(x)的单调递增区间;
(2)当x∈[0,
]时,求f(x)的值域.
| a |
| b |
| 3 |
| a |
| b |
(1)求f(x)的单调递增区间;
(2)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)先利用二倍角公式和两角和公式对函数解析式进行化简,根据三角函数的单调性求得函数单调增区间.
(2)根据x的范围确定2x-
的范围,继而根据余弦函数的图象与性质求得起最大和最小值.
(2)根据x的范围确定2x-
| π |
| 3 |
解答:
解:(1)f(x)=cos2x+
sinxcosx=
(cos2x+1)+
sin2x=cos2xcos
+sin2x•sin
+
=cos(2x-
)+
,
当2x-
∈[2kπ+π,2kπ+2π],k∈Z,时,f(x)单调增,
x∈[kπ+
,π+
],k∈Z,
∴函数f(x)的单调增区间为[kπ+
,π+
],k∈Z,
(2)当x∈[0,
]时,2x-
∈[-
,
],令u=2x-
,f(x)=cosu+
函数f(x)在[-
,0]上递增,在[0,
]上递减,
∴cos(-
)=
,cos0=1,cos
=-
,
∴x当∈[0,
]时,f(x)的值域为[0,
].
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
当2x-
| π |
| 3 |
x∈[kπ+
| 2π |
| 3 |
| 7π |
| 6 |
∴函数f(x)的单调增区间为[kπ+
| 2π |
| 3 |
| 7π |
| 6 |
(2)当x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
函数f(x)在[-
| π |
| 3 |
| 2π |
| 3 |
∴cos(-
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
∴x当∈[0,
| π |
| 2 |
| 3 |
| 2 |
点评:本题主要考察了三角函数恒等变换的应用,三角函数图象与性质.考察了学生综合素质的体现.

练习册系列答案
相关题目
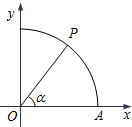 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α. 如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第一群,第二群,…,第n群,…,第n群恰好n个数,则第n群中n个数的和是
如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第一群,第二群,…,第n群,…,第n群恰好n个数,则第n群中n个数的和是