题目内容
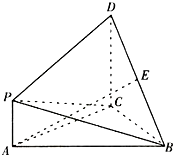 如图,△ABC是等边三角形,PA⊥平面ABC,DC∥PA,且DC=AC=2PA=2,E是BD的中点.
如图,△ABC是等边三角形,PA⊥平面ABC,DC∥PA,且DC=AC=2PA=2,E是BD的中点.(Ⅰ)求证:AE⊥BC;
(Ⅱ)求点D到平面PBC的距离.
考点:点、线、面间的距离计算
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取BC的中点F,连接EF,AF,则EF∥DC,证明BC⊥平面AEF,可得AE⊥BC;
(Ⅱ)利用VD-PBC=VB-PCD得点D到平面PBC的距离.
(Ⅱ)利用VD-PBC=VB-PCD得点D到平面PBC的距离.
解答:
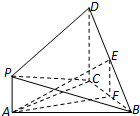 (Ⅰ)证明:取BC的中点F,连接EF,AF,则EF∥DC,…(2分)
(Ⅰ)证明:取BC的中点F,连接EF,AF,则EF∥DC,…(2分)
∵DC⊥平面ABC,∴DC⊥BC,则EF⊥BC;
由△ABC是等边三角形知,AF⊥BC,
∴BC⊥平面AEF,…(4分)
∵AE?平面AEF,∴AE⊥BC. …(6分)
(Ⅱ)取AC的中点H,连接BH,
∴BH⊥AC,又∵平面PACD⊥平面ABC,
∴BH⊥平面PACD,且BH=
;
又PA⊥平面ABC,PA∥DC,DC⊥平面ABC,则,PA⊥AC,…(8分)
由AB=AC=DC=2PA=2知,S△PCD=
DC•AC=2,
∴VB-PCD=
S△PCD•BE=
×2×
=
在Rt△PAF中,可求PF=2,S△PBC=
BC•PF=2; …(10分)
设点D到平面PBC的距离为h,由VD-PBC=VB-PCD得:
S△PBC•h=
,∴h=
,
即点D到平面PBC的距离为
. …(12分)
 (Ⅰ)证明:取BC的中点F,连接EF,AF,则EF∥DC,…(2分)
(Ⅰ)证明:取BC的中点F,连接EF,AF,则EF∥DC,…(2分)∵DC⊥平面ABC,∴DC⊥BC,则EF⊥BC;
由△ABC是等边三角形知,AF⊥BC,
∴BC⊥平面AEF,…(4分)
∵AE?平面AEF,∴AE⊥BC. …(6分)
(Ⅱ)取AC的中点H,连接BH,
∴BH⊥AC,又∵平面PACD⊥平面ABC,
∴BH⊥平面PACD,且BH=
| 3 |
又PA⊥平面ABC,PA∥DC,DC⊥平面ABC,则,PA⊥AC,…(8分)
由AB=AC=DC=2PA=2知,S△PCD=
| 1 |
| 2 |
∴VB-PCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
在Rt△PAF中,可求PF=2,S△PBC=
| 1 |
| 2 |
设点D到平面PBC的距离为h,由VD-PBC=VB-PCD得:
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
即点D到平面PBC的距离为
| 3 |
点评:本题主要考查了直线与平面垂直的判定,以及点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“a>b”是“log3a>log3b”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
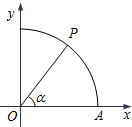 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.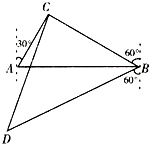 某海域设立东西方向两个观测点A、B,相距
某海域设立东西方向两个观测点A、B,相距