题目内容
7.已知$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(3,-4),当k为何值时(1)k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$共线.
(2)k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$垂直.
分析 (1)利用向量共线定理即可得出.
(2)利用向量垂直与数量积的关系即可得出.
解答 解:(1)k$\overrightarrow{a}$-$\overrightarrow{b}$=(k-3,3k+4),$\overrightarrow{a}$+$\overrightarrow{b}$=(4,-1).
∵k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$共线,∴-(k-3)-4(3k+4)=0,解得k=-1.
(2)∵k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$垂直,∴4(k-3)-(3k+4)=0,解得k=16.
点评 本题考查了向量共线定理、向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
15.平面直角坐标系中,在由x轴、$x=\frac{π}{3}$、x=$\frac{5π}{3}$和y=2所围成的矩形中任取一点,满足不等关系y≤1-sin3x的概率是( )
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.“函数f(x)=a+lnx(x≥e)存在零点”是“a<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不用必要条件 |
1.y=tanx的导数是( )
| A. | $\frac{1}{{{{cos}^2}x}}$ | B. | $-\frac{1}{{{{cos}^2}x}}$ | C. | $\frac{cos2x}{{{{cos}^2}x}}$ | D. | $-\frac{cos2x}{{{{cos}^2}x}}$ |
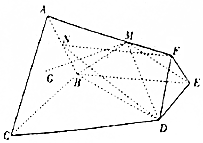 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.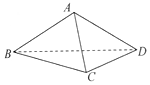 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )