题目内容

在Rt△ABC中，CD是斜边上的高线，AC：BC=3：1，则S△ABC：S△ACD=
 
．
考点：平行线分线段成比例定理
专题：选作题,立体几何
分析：先设BC=a，则AC=3a，AB=
10
a，求出BD，CD的长，即可求出S△ABC：S△BCD，进而求出结论．
解答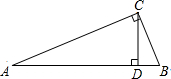： 解：设BC=a，则AC=3a，AB=
10
a，
∵BC2=BD•BA，
∴BD=
BC2
AB
=
10
10
a．
∴CD=
CB2-BD2
=
3
10
10
a．
∴S△ABC：S△BCD=（
1
2
CB•CB•AC）：（
1
2
CB•BD•DC）=10：1，
∴S△ABC：S△ACD=10：9．
故答案为：10：9．
点评：本题主要考查直角三角形的射影定理的应用．考查计算能力，属于基础题目．
练习册系列答案
相关题目
已知椭圆E的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），A（-a，b），B（0，-b），其长轴长是短轴长的两倍，焦距为2
3
．
（Ⅰ）（ⅰ）求椭圆的标准方程；
（ⅱ）求椭圆上到直线AB距离为
2
5
5
的点的个数；
（Ⅱ）过线段AB上的点H作与AB垂直的直线l，交椭圆于P、Q两点，求△OPQ面积的最大值，并求此时直线l的方程．
在平面直角坐标系xOy中，直线y=x+b是曲线y=alnx的切线，则当a＞0时，实数b的最小值是
 
．
从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．从身高在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人选两人当正负队长，则这两人身高不在同一组内的概率为
 
已知点A（a，1）与点B（a+1，3）位于直线x-y+1=0的两侧，则a的取值范围是
 
．
已知函数y=log2x，则在点（1，0）作函数图象的切线，切线方程为
 
．
已知向量
a
与
b
的夹角为60°，且|
a
|=|
b
|=1，那么
a
•（
a
+
b
）=
 
．
命题“?x∈R，x2+4x+5≤0”的否定是
 
．
如图，已知⊙O的两条弦AB、CD相交于AB的中点E，且AB=4，DE=CE+3，则CD的长为（　　）
A、4cmB、2cm
C、5cmD、6cm

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网