题目内容
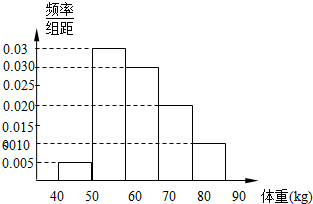
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人选两人当正负队长,则这两人身高不在同一组内的概率为

考点:古典概型及其概率计算公式,频率分布直方图
专题:计算题,概率与统计
分析:由题意,可先计算出身高在[60,70),[70,80),[80,90]三组的频率,计算出12人中各组应抽取的人数,再计算出概率即可.
解答:
解:由图知,身高在[60,70),[70,80),[80,90]三组的频率分别为0.3,0.2,0.1,
故各组的人数分别为30,20,10,
用分层抽样的方法从三组中抽取12人,每组被抽取的人数分别为6,4,2,
从这12人选两人当正负队长,总的抽取方法是12×11=132种
这两人身高不在同一组内的抽取方法是6×4+6×2+4×2=24+12+8=44种,
故这两人身高不在同一组内的概率为
=
.
故答案为
故各组的人数分别为30,20,10,
用分层抽样的方法从三组中抽取12人,每组被抽取的人数分别为6,4,2,
从这12人选两人当正负队长,总的抽取方法是12×11=132种
这两人身高不在同一组内的抽取方法是6×4+6×2+4×2=24+12+8=44种,
故这两人身高不在同一组内的概率为
| 44 |
| 132 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:本题考查古典概率计算及频率分布直方图,分层抽样的方法,有一定的综合性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目