题目内容
已知椭圆E的方程为
+
=1(a>b>0),A(-a,b),B(0,-b),其长轴长是短轴长的两倍,焦距为2
.
(Ⅰ)(ⅰ)求椭圆的标准方程;
(ⅱ)求椭圆上到直线AB距离为
的点的个数;
(Ⅱ)过线段AB上的点H作与AB垂直的直线l,交椭圆于P、Q两点,求△OPQ面积的最大值,并求此时直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)(ⅰ)求椭圆的标准方程;
(ⅱ)求椭圆上到直线AB距离为
2
| ||
| 5 |
(Ⅱ)过线段AB上的点H作与AB垂直的直线l,交椭圆于P、Q两点,求△OPQ面积的最大值,并求此时直线l的方程.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)(ⅰ)由已知c=
,a=2b,可求b,从而可得a,即可求椭圆的标准方程;
(ⅱ)求出椭圆的与AB平行的切线方程,可得到直线AB距离为
的点的个数;
(Ⅱ)直线l方程为y=2x+t(-1≤t≤4)代入椭圆方程,求出|PQ|,O到直线l距离,可得△OPQ面积,利用基本不等式可得最大值,从而可得此时直线l的方程.
| 3 |
(ⅱ)求出椭圆的与AB平行的切线方程,可得到直线AB距离为
2
| ||
| 5 |
(Ⅱ)直线l方程为y=2x+t(-1≤t≤4)代入椭圆方程,求出|PQ|,O到直线l距离,可得△OPQ面积,利用基本不等式可得最大值,从而可得此时直线l的方程.
解答:
解:(Ⅰ)(ⅰ)由已知c=
,a=2b--------------------------(1分)
∴4b2=b2+3,
∴b2=1-----------(2分)
∴a2=4,
∴椭圆的标准方程为
+y2=1-;----------------(4分)
(ⅱ)由题意A(-2,0),B(0,-1),
直线AB的方程为lAB:x+2y+2=0-------------------------(5分)
设椭圆的与AB平行的切线为:x+2y+m=0
代入椭圆方程得:2x2+2mx+m2-4=0
∴△=4m2-8(m2-4)=0,∴m=±2
得切线方程l1:x+2y+2
=0,l2:x+2y-2
=0------------(6分)
l1与lAB距离d1=
<
,
l2与lAB距离d2=
,
故符合题意的点有2个-----------------------------------------------------------(8分)
(Ⅱ)设A(x1,y1),B(x2,y2),直线l方程为y=2x+t(-1≤t≤4)代入椭圆方程
得:17x2+16tx+4(t2-1)=0
∴|PQ|=
•
=
•
-------------------------------------(9分)
∵O到直线l距离为d=
-------------------------------------------(10分)
∴△OPQ面积=
d|PQ|=
•
|PQ|=
≤
•
=1-------------(11分)
此时17-t2=t2,∴t=
此时直线方程为y=2x+
-------------------------------------(12分)
| 3 |
∴4b2=b2+3,
∴b2=1-----------(2分)
∴a2=4,
∴椭圆的标准方程为
| x2 |
| 4 |
(ⅱ)由题意A(-2,0),B(0,-1),
直线AB的方程为lAB:x+2y+2=0-------------------------(5分)
设椭圆的与AB平行的切线为:x+2y+m=0
代入椭圆方程得:2x2+2mx+m2-4=0
∴△=4m2-8(m2-4)=0,∴m=±2
| 2 |
得切线方程l1:x+2y+2
| 2 |
| 2 |
l1与lAB距离d1=
2(
| ||
| 5 |
2
| ||
| 5 |
l2与lAB距离d2=
2(
| ||
|
故符合题意的点有2个-----------------------------------------------------------(8分)
(Ⅱ)设A(x1,y1),B(x2,y2),直线l方程为y=2x+t(-1≤t≤4)代入椭圆方程
得:17x2+16tx+4(t2-1)=0
∴|PQ|=
| 5 |
| (x1+x2)2-4x1x2 |
4
| ||
| 17 |
| 17-t2 |
∵O到直线l距离为d=
| |t| | ||
|
∴△OPQ面积=
| 1 |
| 2 |
| 1 |
| 2 |
| |t| | ||
|
| 2 |
| 17 |
| t2(17-t2) |
| 2 |
| 17 |
| 17-t2+t2 |
| 2 |
此时17-t2=t2,∴t=
| ||
| 2 |
此时直线方程为y=2x+
| ||
| 2 |
点评:本题中考查了椭圆的方程及其性质、直线与椭圆相交问题转化为一元二次方程的根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、基本不等式的性质等基础知识与基本技能,考查了分析问题和解决问题的能力、推理能力和计算能力.

练习册系列答案
相关题目
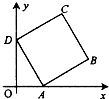 如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则
如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则