题目内容
AB为过椭圆
+
=1中心的弦，F（c，0）为它的焦点，则△FAB的最大面积为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、b2 | B、ab |
| C、ac | D、bc |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据题意设A（x0，y0），B（-x0，-y0），表示出直线AB的方程，求出|AB|，及点F到直线AB的距离，表示出面积S=|y0|c，所以当|y0|取最大值b时，△FAB的面积最大，并且最大为bc．
解答：
解：设A（x0，y0），则B（-x0，-y0），直线AB的方程为：y=
x；
∴|AB|=2
，F到AB的距离为：
=
；
∴△FAB的面积为：S=
•2
•
=c|y0|；
∵-b≤y0≤b，∴|y0|=b时，S取最大值bc．
故选D．
| y0 |
| x0 |
∴|AB|=2
| x02+y02 |
|c
| ||||
|
| c|y0| | ||
|
∴△FAB的面积为：S=
| 1 |
| 2 |
| x02+y02 |
| c|y0| | ||
|
∵-b≤y0≤b，∴|y0|=b时，S取最大值bc．
故选D．
点评：考查椭圆的几何性质：图形关于原点对称，直线的点斜式方程，点到直线的距离公式，两点间距离公式．
练习册系列答案
相关题目
已知函数f（x）=logax（0＜a＜1）的导函数f′（x），A=f′（a），b=f（a+1）-f（a），C=f′（a+1），D=f（a+2）-f（a+1），则A，B，C，D中最大的数是（ ）
| A、A | B、B | C、C | D、D |
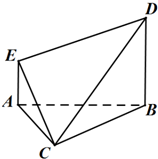如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1．