题目内容
如果直线l将圆C：（x-2）2+（y+3）2=13平分，那么坐标原点O到直线l的最大距离为 ．
考点：直线与圆的位置关系
专题：圆锥曲线的定义、性质与方程
分析：先考虑斜率不存在时，的情况，再看斜率存在时，设出直线的方程，利用点到直线的距离建立关于k的一元二次方程，利用判别式法求得d的范围．
解答：
解：当直线的斜率不存在时，直线的方程为x=2，原点到直线l的距离为2，
当斜率存在时，设为k，则直线的方程为y+3=k（x-2），整理得kx-y-2k-3=0，
原点到直线l的距离d=
，
d2=
，整理得（4-d2）k2+12k+9-d=0，
△=144-4（4-d2）（9-d）≥0，
求得0＜d≤
，
故坐标原点O到直线l的最大距离为
．
故答案为：
当斜率存在时，设为k，则直线的方程为y+3=k（x-2），整理得kx-y-2k-3=0，
原点到直线l的距离d=
| |2k+3| | ||
|
d2=
| (2k+3)2 |
| 1+k2 |
△=144-4（4-d2）（9-d）≥0，
求得0＜d≤
| 13 |
故坐标原点O到直线l的最大距离为
| 13 |
故答案为：
| 13 |
点评：本题主要考查了直线的位置关系．解题的过程中不要忘了斜率不存在的情况．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
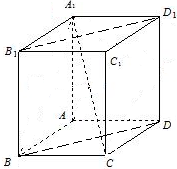已知长方体A1B1C1D1-ABCD的高为
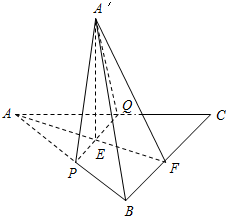如图所示，等边△ABC的边长为a，将它沿平行于BC的线段PQ折起，使平面A′PQ⊥平面BPQC，若折叠后A′B的长为d，则d的最小值为椭圆的焦点坐标为（4，0），（-4，0），椭圆上一点到两焦点的距离之和为10，则椭圆的标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|