题目内容
已知直线l的方程3x+4y-12=0,求与l垂直且与两坐标轴围成的三角形的面积为4的直线方程.
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:根据垂直关系求出直线的额斜率,得到它在坐标轴上的截距,根据与两坐标轴围成的三角形面积为4 求出截距,即得直线方程.
解答:
解:∵直线l的方程3x+4y-12=0,
∴设所求直线l′的方程为y=
x+b,
∴直线l′在x轴上的截距为-
b,在y轴上的截距为b,
∵与l垂直且与两坐标轴围成的三角形的面积为4,
∴S=
|b||-
b|=4,
解得b=±
,
∴所求的直线方程为y=
x+
或y=
x-
.
∴设所求直线l′的方程为y=
| 4 |
| 3 |
∴直线l′在x轴上的截距为-
| 3 |
| 4 |
∵与l垂直且与两坐标轴围成的三角形的面积为4,
∴S=
| 1 |
| 2 |
| 3 |
| 4 |
解得b=±
| 4 |
| 3 |
| 6 |
∴所求的直线方程为y=
| 4 |
| 3 |
| 4 |
| 3 |
| 6 |
| 4 |
| 3 |
| 4 |
| 3 |
| 6 |
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意直线性质的合理运用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
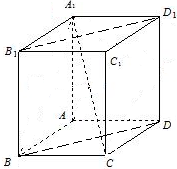 已知长方体A1B1C1D1-ABCD的高为
已知长方体A1B1C1D1-ABCD的高为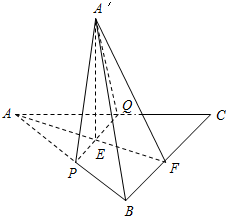 如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为
如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为