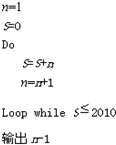题目内容
灯泡厂生产的白炽灯泡的寿命为X，已知X～N（1000，302）．要使灯泡的平均寿命为1000小时的概率为99.7%，问灯泡的最低寿命应控制在多少小时以上？
考点：正态分布曲线的特点及曲线所表示的意义
专题：概率与统计
分析：由于灯泡的寿命为X，X～N（1000，302）．可得X在（1000-3×30，1000+3×30）的概率为99.7%，即可得出．
解答：
解：∵灯泡的寿命为X，X～N（1000，302）．
∴X在（1000-3×30，1000+3×30）的概率为99.7%，
∴X在（910，1090）内的取值的概率为99.7%，
∴X在（1000-3×30，1000+3×30）的概率为99.7%，
∴X在（910，1090）内的取值的概率为99.7%，
点评：本题考查了正态分布的“3σ原则”，属于基础题．
练习册系列答案
相关题目
S=1+（1+2）+（1+2+22）+…+（1+2+22+…+210）的值是（ ）
| A、211-11 |
| B、211-13 |
| C、212-13 |
| D、213-11 |
过点M（0，1）与抛物线y2=2x只有一个公共点的直线有（ ）
| A、1条 | B、2条 | C、3条 | D、0条 |
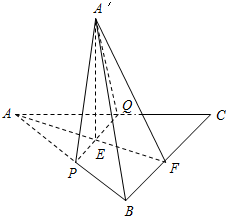如图所示，等边△ABC的边长为a，将它沿平行于BC的线段PQ折起，使平面A′PQ⊥平面BPQC，若折叠后A′B的长为d，则d的最小值为