题目内容
已知函数f(x)=lnx+
-1.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.
| 1 |
| x |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求出函数的导数,令f'(x)>0,得到函数f(x)的单调递增区间,令f'(x)<0,得到函数f(x)的单调递减区间;
(Ⅱ)求出函数最大值,得不等式组
,解出即可.
(Ⅱ)求出函数最大值,得不等式组
|
解答:
解:(Ⅰ)∵f′(x)=
-
=
,x>0,
令f'(x)>0,得x>1,因此函数f(x)的单调递增区间是(1,+∞),
令f'(x)<0,得0<x<1,因此函数f(x)的单调递减区间是(0,1).
(Ⅱ)依题意,ma<f(x)max,由(Ⅰ)知,f(x)在x∈[1,e]上是增函数,
∴f(x)max=f(e)=lne+
-1=
,
∴ma<
,即ma-
<0对于任意的a∈(-1,1)恒成立,
∴
,解得-
≤m≤
,
∴m的取值范围是[-
,
].
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
令f'(x)>0,得x>1,因此函数f(x)的单调递增区间是(1,+∞),
令f'(x)<0,得0<x<1,因此函数f(x)的单调递减区间是(0,1).
(Ⅱ)依题意,ma<f(x)max,由(Ⅰ)知,f(x)在x∈[1,e]上是增函数,
∴f(x)max=f(e)=lne+
| 1 |
| e |
| 1 |
| e |
∴ma<
| 1 |
| e |
| 1 |
| e |
∴
|
| 1 |
| e |
| 1 |
| e |
∴m的取值范围是[-
| 1 |
| e |
| 1 |
| e |
点评:本题考查了函数的单调性问题,函数的最值问题,考查了导数的应用,是一道中档题.

练习册系列答案
相关题目
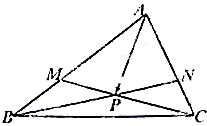 在△ABC中,点M、N分别在边AB、AC上,且
在△ABC中,点M、N分别在边AB、AC上,且| AM |
| MB |
| AN |
| 3 |
| 5 |
| AC |
| AB |
| a |
| AC |
| b |
| AP |
| a |
| b |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
过原点的直线交双曲线xy=
于P、Q两点,现将坐标平面沿x轴折成直二面角,则折后线段PQ的长度的最小值等于( )
| 2 |
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
某几何体的三视图如图所示,则该几何体的表面积为( )


A、6+2
| ||
B、
| ||
| C、8 | ||
D、4(1+
|