题目内容
给出下列三个命题:
①若△ABC三边为a,b,c,面积为S,内切圆的半径r=
,则由类比推理知四面体ABCD的内切球半径R=
(其中,V为四面体的体积,为S1,S2,S3,S4四个面的面积);
②若回归直线的斜率估计值是1.23,样本点的中心为(4,5),则回归直线方程是
=1.23x+0.08;
③用相关系数r来刻画回归效果,r2越小,说明模型的拟合效果越好.
其中,正确命题的序号是 .(把你认为正确命题的序号都填上)
①若△ABC三边为a,b,c,面积为S,内切圆的半径r=
| 2S |
| a+b+c |
| 3V |
| S1+S2+S3+S4 |
②若回归直线的斜率估计值是1.23,样本点的中心为(4,5),则回归直线方程是
| ∧ |
| y |
③用相关系数r来刻画回归效果,r2越小,说明模型的拟合效果越好.
其中,正确命题的序号是
考点:命题的真假判断与应用
专题:概率与统计,推理和证明
分析:①设四面体的内切球的球心为O,则球心O到四个面的距离都是R,由V四面体A-BCD=
(S1+S2+S3+S4)•R,可得R=
,从而可判断①正确;
②设回归直线方程是
=1.23x+b,将样本中心(4,5)的坐标代入回归直线方程得b的值,从而可判断②的正误;
③用相关系数r来刻画回归效果,|r|的值越大,说明模型拟合的效果越好,从而可判断③之正误.
| 1 |
| 3 |
| 3V |
| S1+S2+S3+S4 |
②设回归直线方程是
| ∧ |
| y |
③用相关系数r来刻画回归效果,|r|的值越大,说明模型拟合的效果越好,从而可判断③之正误.
解答:
解:①设四面体的内切球的球心为O,则球心O到四个面的距离都是R,
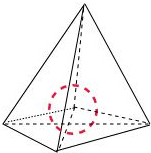
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为V四面体A-BCD=
(S1+S2+S3+S4)•R,
∴R=
,即①正确;
②若回归直线的斜率估计值是1.23,样本点的中心为(4,5),设回归直线方程是
=1.23x+b,
将样本点中心(4,5)的坐标代入回归直线方程得:5=1.23×4+b,
解得b=0.08,故回归直线方程是
=1.23x+0.08,即②正确;
③用相关系数r来刻画回归效果,|r|的值越大,说明模型拟合的效果越好,故③错误.
综上所述,正确命题的序号是①②,
故答案为:①②.

所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为V四面体A-BCD=
| 1 |
| 3 |
∴R=
| 3V |
| S1+S2+S3+S4 |
②若回归直线的斜率估计值是1.23,样本点的中心为(4,5),设回归直线方程是
| ∧ |
| y |
将样本点中心(4,5)的坐标代入回归直线方程得:5=1.23×4+b,
解得b=0.08,故回归直线方程是
| ∧ |
| y |
③用相关系数r来刻画回归效果,|r|的值越大,说明模型拟合的效果越好,故③错误.
综上所述,正确命题的序号是①②,
故答案为:①②.
点评:本题考查命题的真假判断与应用,着重考查类比推理与线性相关关系的应用,考查推理与运算能力,属于中档题.

练习册系列答案
相关题目
将函数y=5sin3x的图象向左平移
个单位,得到的图象的解析式是( )
| π |
| 3 |
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |

