题目内容
已知x>0,y>0,且
+
=4,则x+2y最小值是 .
| 2 |
| x |
| 1 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:先把x+2y转化为
(
+
)(x+2y)的形式,展开后利用基本不等式求得其最小值.
| 1 |
| 4 |
| 2 |
| x |
| 1 |
| y |
解答:
解:x+2y=
(
+
)(x+2y)=
(4+
+
)≥
(4+2
)=2,
故答案为:2.
| 1 |
| 4 |
| 2 |
| x |
| 1 |
| y |
| 1 |
| 4 |
| 4y |
| x |
| x |
| y |
| 1 |
| 4 |
| 4 |
故答案为:2.
点评:本题主要考查了基本不等式的应用.解题的关键是把原式转化为
(
+
)(x+2y)的形式,进而利用基本不等式的知识来解决.
| 1 |
| 4 |
| 2 |
| x |
| 1 |
| y |

练习册系列答案
相关题目
在区间[0,6]上随机取一个数x,log2x的值介于1到2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
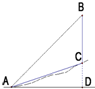 如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为
如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为