题目内容
16.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )| A. | 0 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 先根据|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),求出2$\overrightarrow{a}$•$\overrightarrow{b}$=1,再求出|$\overrightarrow{a}$+$\overrightarrow{b}$|2,问题得以解决.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),
∴$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴2$\overrightarrow{a}$•$\overrightarrow{b}$=1,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=1+1+1=3,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,
故选:D.
点评 本题考查了向量的数量积运算和模的计算以及向量垂直的条件,属于基础题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案| A. | (0,3) | B. | (-∞,3] | C. | [3,+∞) | D. | [3,4) |
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
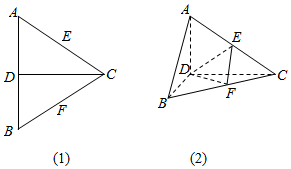 如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))
如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))