题目内容
4.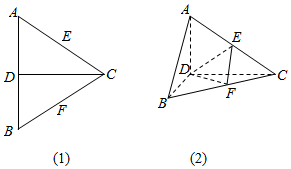 如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))
如图(1),正三角形ABC边长为2a,CD是AB边上的高,E,F分别为AC和BC边上的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))(1)请判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B-AC-D的大小;
(3)求点C到平面DEF的距离.
分析 (1)判断AB∥平面DEF,再由直线与平面平行的判定定理进行证明.
(2)以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AC-D的大小.
(3)先求出平面DEF的法向量,由此能求出点C到平面DEF的距离.
解答  解:(1)判断:AB∥平面DEF,
解:(1)判断:AB∥平面DEF,
证明:在△ABC中,E,F分别是AC,BC的中点,
∴EF∥AB,
又AB?平面DEF,EF?平面DEF,
∴AB∥平面DEF.
(2)以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
B(a,0,0),A(0,0,a),C(0,$\sqrt{3}a$,0),D(0,0,0),
$\overrightarrow{AB}$=(a,0,-a),$\overrightarrow{AC}$=(0,$\sqrt{3}a$,-a),
设平面ABC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=ax-az=0}\\{\overrightarrow{n}•\overrightarrow{AC}=\sqrt{3}ay-az=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3}$,1,$\sqrt{3}$),
又平面ACD的法向量$\overrightarrow{m}$=(1,0,0),
设二面角B-AC-D的大小为α,
则cosα=|cos<$\overrightarrow{n},\overrightarrow{m}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
∴二面角B-AC-D的大小为arccos$\frac{\sqrt{21}}{7}$.
(3)C(0,$\sqrt{3}a$,o),E(0,$\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$),F($\frac{a}{2}$,$\frac{\sqrt{3}a}{2}$,0),D(0,0,0),
$\overrightarrow{DC}$=(0,$\sqrt{3}a$,0),$\overrightarrow{DE}$=(0,$\frac{\sqrt{3}a}{2}$,$\frac{a}{2}$),$\overrightarrow{DF}$=($\frac{a}{2},\frac{\sqrt{3}a}{2}$,0),
设平面DEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=\frac{\sqrt{3}a}{2}y+\frac{a}{2}z=0}\\{\overrightarrow{n}•\overrightarrow{DF}=\frac{a}{2}x+\frac{\sqrt{3}a}{2}y=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3}$,-1,$\sqrt{3}$),
∴点C到平面DEF的距离d=$\frac{|\overrightarrow{DC}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{\sqrt{3}a}{\sqrt{7}}$=$\frac{\sqrt{21}a}{7}$.
点评 本题考查直线与平面的位置关系的判断,考查二面角、点到平面距离的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

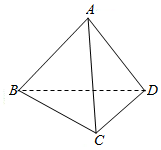 在空间四边形ABCD中,AB=AC=AD=1
在空间四边形ABCD中,AB=AC=AD=1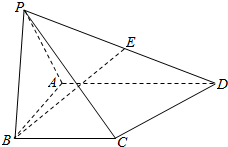 如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.
如图所示,在四棱锥P-ABCD中,△PAB为等边三角形,AD⊥AB,AD∥BC,平面PAB⊥平面ABCD,E为PD的中点.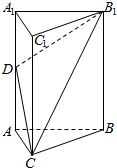 如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.
如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.