题目内容
11.关于x的方程102x-4×10x+2t=0有两不等实根,则$\frac{{t}^{2}+t+4}{t+1}$的取值范围是( )| A. | (0,3) | B. | (-∞,3] | C. | [3,+∞) | D. | [3,4) |
分析 利用换元法将方程转化为一元二次方程,求出t的取值范围,然后利用分式函数的性质,再利用分子常数化,利用对勾函数的单调性进行求解即可.
解答 解:∵102x-4×10x+2t=0,
∴设m=10x,m>0,
得方程等价为m2-4m+2t=0有两个不同的正根,
则$\left\{\begin{array}{l}{△=16-8t>0}\\{{m}_{1}+{m}_{2}=4>0}\\{{m}_{1}{m}_{2}=2t>0}\end{array}\right.$,即$\left\{\begin{array}{l}{t<2}\\{t>0}\end{array}\right.$,即0<t<2,
则$\frac{{t}^{2}+t+4}{t+1}$=$\frac{(t+1)^{2}-(t+1)+4}{t+1}$=t+1+$\frac{4}{t+1}$-1,
设a=t+1,则1<a<3,则t+1+$\frac{4}{t+1}$-1=a+$\frac{4}{a}$-1
则函数y=a+$\frac{4}{a}$-1在(1,2]上单调递减,在[2,3)上单调递增,
当a=2时,函数取得最小值y=2+2-1=3,
当a=1时,y=1+4-1=4,
当a=3时,y=3+$\frac{4}{3}$-1=$\frac{10}{3}$,
即3≤y<4,
即$\frac{{t}^{2}+t+4}{t+1}$的取值范围是[3,4),
故选:D
点评 本题主要考查函数与方程的应用,利用换元法和转化法将方程转化为一元二次方程以及对勾函数形式是解决本题的关键.综合考查学生的运算能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.函数y=5sin2x+12cos2x的最小值和周期分别是( )
| A. | 5,π | B. | ,12,π | C. | ,-13,π | D. | -13,2π |
16.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | 0 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
4.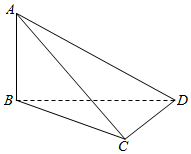 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.