题目内容
9.已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点,(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于3?若存在,求出直线l的方程;若不存在,请说明理由.
分析 (Ⅰ)依题意,可设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),由椭圆C经过点A(2,3),且点F(2,0)为其右焦点,利用椭圆定义及性质列出方程组,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)假设存在符合题意的直线l,其方程为y=$\frac{3}{2}x+t$,与椭圆联立得到3x2+3tx+t2-12=0,由此利用根的判别式、点到直线距离公式能求出直线l的方程.
解答 解:(Ⅰ)依题意,可设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
∵点F(2,0)为椭圆C的右焦点,∴左焦点为F1(-2,0),
∴$\left\{\begin{array}{l}{c=2}\\{2a=|AF|+|A{F}_{1}|=3+5=8}\end{array}\right.$,解得a=4,c=2,
又a2=b2+c2,所以b2=12,
故椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
(Ⅱ)假设存在符合题意的直线l,其方程为y=$\frac{3}{2}x+t$,
由$\left\{\begin{array}{l}{y=\frac{3}{2}x+t}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,解得3x2+3tx+t2-12=0,
∵直线l与椭圆C有公共点,∴△=(3t)2-4×3(t2-12)≥0,
解得-4$\sqrt{3}$$≤t≤4\sqrt{3}$,
另一方面,由直线OA与l的距离d=3,得$\frac{|t|}{\sqrt{\frac{9}{4}+1}}$=3,
解得t=±$\frac{\sqrt{39}}{2}$,
∵$±\frac{\sqrt{39}}{2}$∈[-4$\sqrt{3}$,4$\sqrt{3}$],
∴符合题意的直线l为y=$\frac{3}{2}x±\frac{\sqrt{39}}{2}$.
点评 本题考查椭圆方程的求法,考查符合条件的直线方程是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、点到直线距离公式的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | 0 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
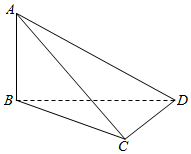 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
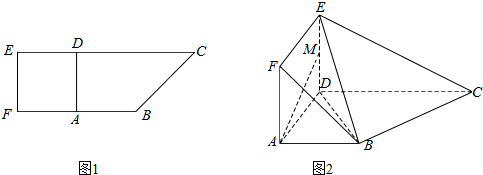
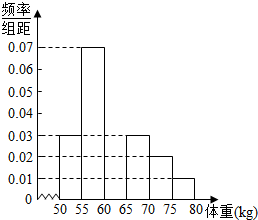 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题: