题目内容
11.A、B是120°二面角α-l-β的棱l上的两点,分别在α,β内作垂直于棱l的线段AC,BD,已知AB=AC=BD=1,那么CD的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 由$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,利用向量法能求出CD的长.
解答 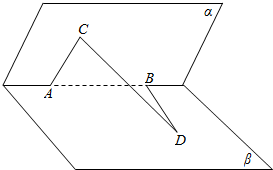 解:∵A、B是120°二面角α-l-β的棱l上的两点,
解:∵A、B是120°二面角α-l-β的棱l上的两点,
分别在α,β内作垂直于棱l的线段AC,BD,AB=AC=BD=1,
∴$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}$=($\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$)2
=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+2$\overrightarrow{CA}•\overrightarrow{BD}$
=1+1+1-2×1×1×$\frac{1}{2}$
=2.
∴CD的长|$\overrightarrow{CD}$|=$\sqrt{2}$.
故选:C.
点评 本题考查线段长的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
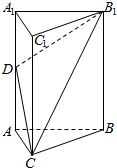 如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.
如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点. 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.